2 Algebra: 2.3 Förenkling av uttryck
 2.3 Förenkling av uttryck
2.3 Förenkling av uttryck
|
Rektangeln har basen #\color{green}{b}# och höjden #\color{red}{h}#.
|
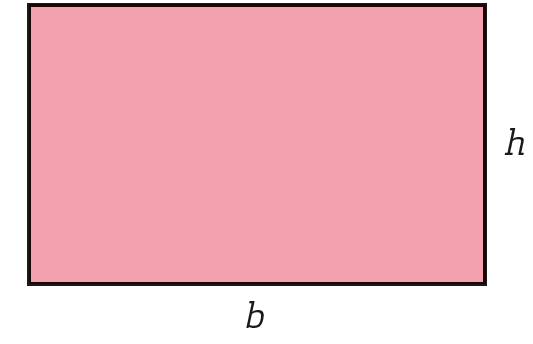 |
#\color{green}{b} + \color{red}{h} + \color{green}{b} + \color{red}{h} =#
#=\color{green}{b} + \color{green}{b} + \color{red}{h} + \color{red}{h} = 2 \,\cdot\, \color{green}{b} + 2 \, \cdot\, \color{red}{h} = 2\color{green}{b} + 2\color{red}{h}#
När man förenklar ett uttryck lägger man samman termer av samma sort till en term.
Man adderar då till exempel b-termer, h-termer och siffertermer för sig.
Lägg märke till att vi skriver #2\,\cdot\,b# som #2b# och #2\,\cdot\,h# som #2h#.
Förenkla uttrycken.
a) #5y+2y \qquad# b) #12x-14x \qquad# c) #5x+3+2x-9 \qquad# d) #a+b-2a-2b+3b#
| a) #5y+2y=7y# | #5y = y + y + y + y + y# och #2y = y + y#. Därför är #5y + 2y = y + y + y + y + y + y + y = 7y# |
| b) #12x-14x=-2x# | Eftersom #12 - 14 = -2# så är #12x - 14x = -2x# |
| c) #\color{red} { \dunderline{ \color{black}{5x}}}\ \color{green} { \dunderline{ \color{black}{+\,3}}} \ \color{red} { \dunderline{ \color{black}{+\,2x}}} \ \color{green} { \dunderline{ \color{black}{-9}}} =# #= \color{red} { \dunderline{ \color{black}{5x + 2x}}}\, \color{green} { \dunderline{ \color{black}{+ 3 - 9}}}# #= 7x - 6# |
Uttrycket innehåller två slags termer, #\color{red} { \dunderline{\color{black}{x-\text{termer}}}}# och #\color{green} { \dunderline{ \color{black}{\text{siffertermer}}}}#. Samla #x#-termerna för sig och siffertermerna för sig. Sen kan du förenkla uttrycket så att det bara blir en #x#-term och en sifferterm kvar. Det är viktigt att du även tar med #+# eller #–# tecknet när du flyttar termer. |
| d) #\color{red}{\dunderline{\color{black}{a}}}\ \color{green}{\dunderline{\color{black}{+\;b}}} \ \color{red}{\dunderline{\color{black}{-2a}}}\ \color{green}{\dunderline{\color{black}{-\, 2b + 3b}}} =# | Observera att #a = a# och #b = b#. Men man brukar utelämna #1#:an. Du får då att #a - 2a = - a = -a# samt #b - 2b + 3b = 2b#. |
| #=\color{red} {\dunderline{\color{black}{a - 2a}}}\ \color{green}{\dunderline{\color{black}{+ \; b - 2b +3b}}} =# | |
| #= - a + 2b =# #=2b - a# |
Om det finns en positiv term i svaret brukar man skriva den först. Byt därför plats på #a#-term och #b#-term. |
| Svar: | a) #7y# c) #7x - 6# |
b) #-2x# d) #2b - a# |
K
|

