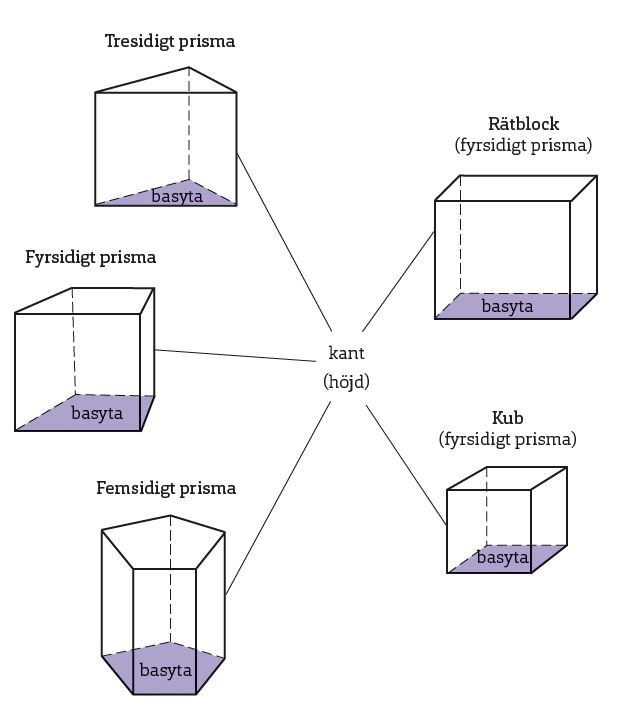
Prisma

Ett prisma har en polygon som basyta. Sidoytorna är rektanglar. Det innebär att till exempel alla rätblock är prismor. Eftersom en kub är ett rätblock är alltså även en kub ett prisma.

Volymen av ett prisma räknas ut genom att basytans area #( B )# multipliceras med höjden #( h )#.

#V = B \cdot h#

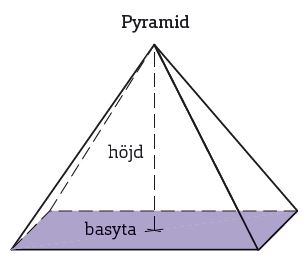
Pyramid

Även i en pyramid är basytan en månghörning, men sidoytorna är trianglar.

Om en pyramid har samma basyta och samma höjd som ett prisma, så är pyramidens volym #1/3# av prismats volym. Formeln för pyramidens volym är alltså:

#V = \frac{B \cdot h}{3}# I formeln är #B =# basytans area och #h =# pyramidens höjd.

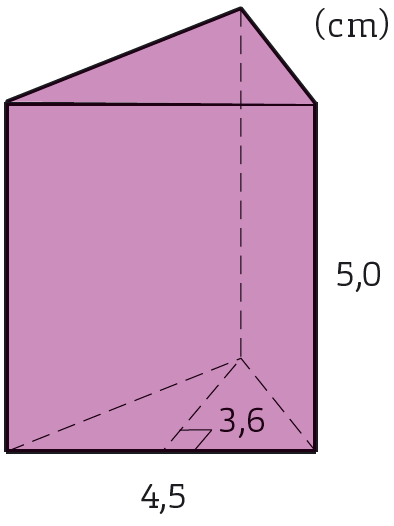
Hur stor är prismats volym? Avrunda till hela kubikcentimeter.

#B = \frac{b \cdot h}{2}#	Eftersom basytan är en triangel beräknas basytans area med formeln #B = \frac{b \cdot h}{2}#.
#B = \frac{4,5 \cdot 3,6}{2}# cm#^2 = 8,1# cm#^2#
#V = B \cdot h#	Lägg märke till att #h# används i två olika betydelser. I formeln #B = \frac{b \cdot h}{2}# är #h# lika med triangelns höjd. I formeln #V = B \cdot h# är #h# lika med prismats höjd.

#V = 8,1 \cdot 5,0# cm#^3 = 40,5# cm#^3 \approx 41# cm#^3#. Svar: Volymen är #41# cm#^3#.

K Skriv formler. Använd #B# för basytans area och #b# för basens längd. Visa dina beräkningar. Svara med hel mening.

Nästa exempel

Hur stor är pyramidens volym? Avrunda till tiondels liter.

#B = b \cdot h#

Här är basytan en rektangel och arean beräknas med formeln #B = b \cdot h#.

#B = 23,5 \cdot 16,4# cm#^2 = 385,4# cm#^2#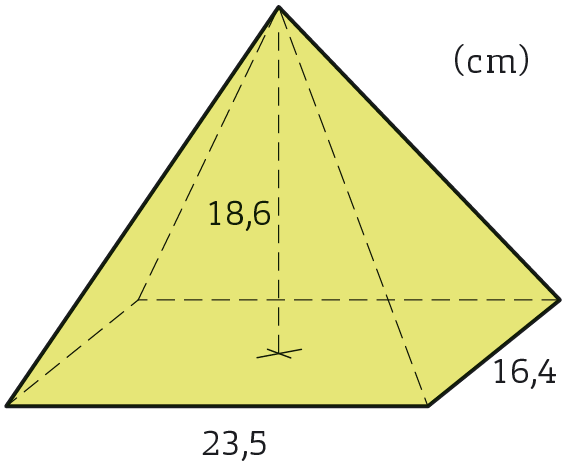

#V = \frac{385,4 \cdot 18,6}{3}# cm#^3 = 2\,389,48# cm#^3 \approx 2\,400# cm#^3 = 2,4# dm#^3 = 2,4# liter

Svar: Volymen är #2,4# liter.

K Skriv formler. Använd #B# för basytans area och #b# för basens längd. Visa dina beräkningar. Ta med enheterna i varje led. Svara med hel mening.

Nästa exempel