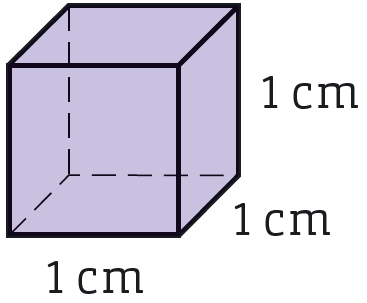
Med volym menas hur stor en kropp är. När man beräknar en kropps volym utgår man ofta från en kub där kanterna är #1# cm. En sådan kub har volymen #1# cm#^3# (en kubikcentimeter). Vi kan räkna ut volymen så här: #1 \text{ cm} \cdot 1 \text{ cm} \cdot 1 \text{ cm} = 1 \cdot 1 \cdot 1 \cdot \text{ cm }\cdot \text{ cm } \cdot \text{ cm } = 1# cm#^3# Eftersom kroppen breder ut sig i tre dimensioner blir enheten i kubik, alltså upphöjt till tre #(#cm#^3)#.

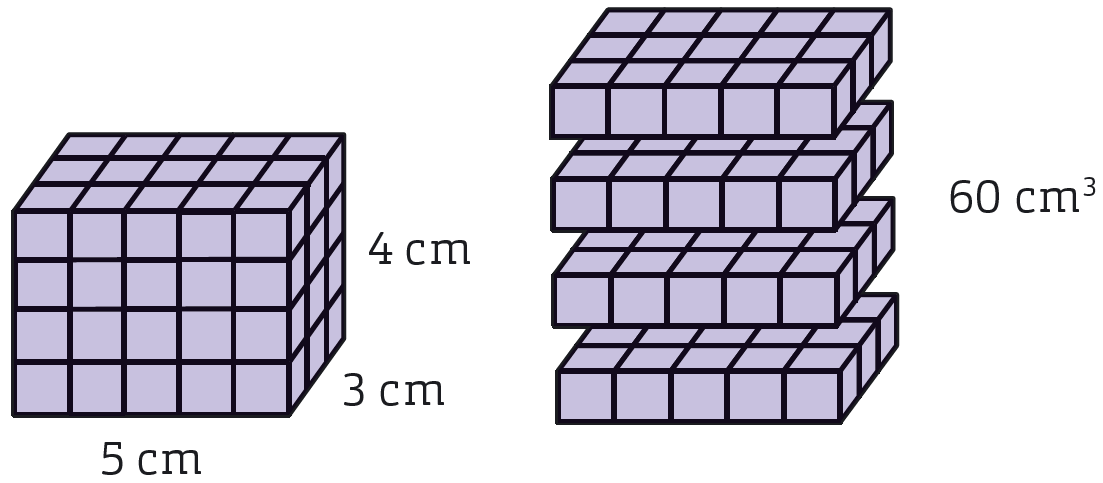
Det här rätblocket har en basyta med arean #5 \cdot 3# cm#^2= 15# cm#^2# . På den ytan kan vi lägga #15# kuber med volymen #1# cm#^3# . Eftersom rätblockets höjd är #4# cm så får det sammanlagt plats #15\cdot4# kuber #= 60# kuber med volymen #1# cm#^3#. Rätblockets volym är alltså #60# cm#^3#. Vi ser att vi kan räkna ut volymen #(V)# genom att multiplicera basytans area #(B)# med höjden #(h)#.

I det här fallet är #B = 5 \cdot 3# cm#^2 = 15# cm#^2# och #h = 4# cm.

Alltså är #V = 15 \cdot 4# cm#^3 = 60# cm#^3#.