Cylinderns mantelyta
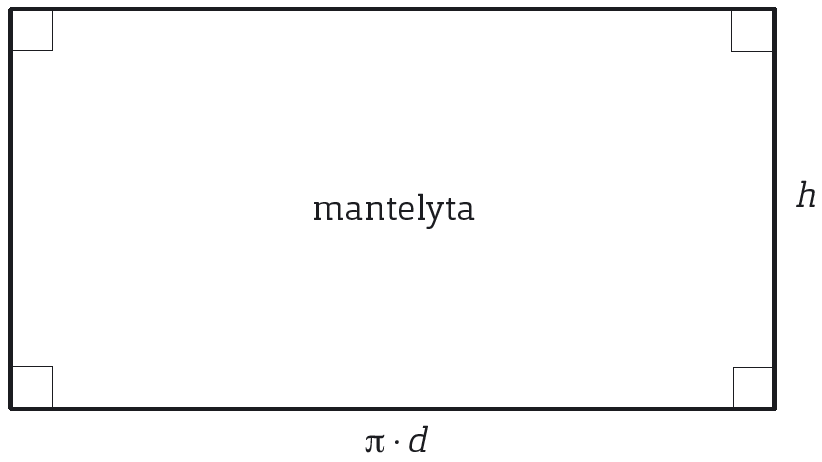
Vi tänker oss att vi klipper upp cylinderns mantelyta längs med höjden. Om vi sen vecklar ut mantelytan får vi en rektangel. Rektangelns bas är lika med basytans omkrets #(\pi \cdot d)#. Rektangelns höjd är lika med cylinderns höjd #(h)#. Mantelytans area #(A)#, den så kallade mantelarean, kan alltså beräknas med formeln:
| #A = \pi \cdot d \cdot h# |
|
|
 |
| Eftersom #d = 2 \cdot r# så kan mantelarean också beräknas med formeln #A = 2\cdot \pi \cdot r \cdot h# |
 |
Hur stor är burkens volym? Avrunda till tiotal kubikcentimeter. |
| #V=B\cdot h# |
|
| #B=\pi\cdot r^2# |
Teckna ett uttryck för arean med hjälp av #\pi#. Men räkna inte ut något närmevärde än. På så sätt undviker du avrundningsfel. |
| #B=\pi\cdot 4^2# cm#^2 = 16 \cdot \pi# cm#^2# |
| #V= 16 \cdot \pi \cdot 17 # cm#^3=854,5\dots # cm#^3\approx 850 # cm#^3# |
| |
Du kan såklart även räkna ut basytans area först. Du får då #\pi \cdot 42 # cm#^2 = 50,265\dots # cm#^2#. Men tänk då på att inte avrunda svaret, utan behåll hela talet i miniräknaren. Nästa steg blir då #50,265 \ldots \cdot 17 # cm#^3 = 854,5 \ldots # cm#^3 \approx 850 # cm#^3# |
| Svar: Volymen är #850# cm#^3#. |
K
- Skriv formler.
- Presentera och teckna dina beräkningar.
- Ta med enheterna i varje led.
- Svara med hel mening.
|
3.6 Cylinderns mantelyta
