9 Elektricitet: 9.3 Spänning
 9.3 Spänning
9.3 Spänning
9.3 Spänning
Ett exempel på ett elektriskt fält är fältet mellan två parallella metallplattor med olika laddning. Se figur 9.7. Ett sådant fält är homogent. Det innebär att fältstyrkan \(E\) har samma riktning och samma storlek överallt i fältet.
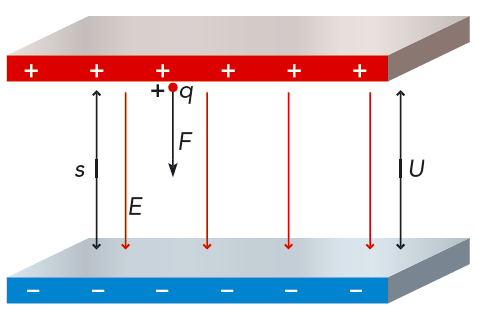
Vad händer nu, om man placerar en positiv laddning \(q\) i det elektriska fältet mellan plattorna?
Eftersom laddningen är positiv så kommer den att påverkas av en elektrisk kraft, \(F = Eq\), mot den negativa plattan. Laddningen kommer då att röra sig mot den negativa plattan och får energin\( W = Fs = Eqs\), där \(s\) är avståndet mellan plattorna. Det elektriska fältet har således utfört ett arbete på den elektriska laddningen som nu har fått rörelseenergin \(W\). Man har valt att kalla energin, eller arbetet, per laddning för elektrisk spänning, \(U\). \[ U = \frac{W}{q} = Es\] där \(U\) är spänningen mellan två punkter som ligger i fältets riktning. Sträckan \(s\) är parallell med fältet.
\[ \text{Spänning} = \frac{\text{arbete}}{\text{laddning}} \ \text{ eller } \ U = \frac{W}{Q} \] Enheten för spänning är volt, \(\text{V}\).
Volt är lika med joule per coulomb, \(1 \text{ V} = 1 \text{ J/C}\). Enheten volt är uppkallad efter den italienske fysikern Alessandro Volta, som konstruerade den första elektriska spänningskällan.
Volta konstruerade det första elektriska batteriet. Andra forskare tog sig an uppfinningen, och snart kunde ett universitet mäta sin status efter spänningen på det elektriska batteri det hade. Med hjälp av batteriet skapade de gnistor och skickade elektricitet genom olika ämnen. Med detta grundlade de en ny gren av fysiken, elektricitetsläran.
Vi ser också att spänningen \(U\) mellan två punkter beskriver fältstyrkan mellan punkterna.
Ur formeln \[ U = \frac{W}{q} = Es \] får vi att den elektriska fältstyrkan \(E = U/s\).
I det homogena elektriska fältet mellan två metallplattor är fältstyrkan \[ \text{Elektrisk fältstyrka} = \frac{\text{spänning}}{\text{avstånd mellan plattorna}} \ \text{ eller} \ E = \frac{U}{s} \] Där \(U\) är spänningen och \(s\) är avståndet mellan plattorna.
Formeln visar oss att enheten för elektrisk fältstyrka också kan skrivas som volt per meter, \(\text{V/m}\). Enheten för fältstyrka har vi hittills skrivit som \(\text{N/C}\). Vi har alltså \[ 1 \text{ N/C} = 1 \text{ V/m}\]
En elektron befinner sig i ett homogent fält mellan två parallella plattor. Spänningen mellan dessa är \(180 \text{ V}\) och avståndet mellan dem \(2{,}5 \text{ cm}\). Hur stor är kraften som påverkar elektronen då den befinner sig \(2 \text{ cm}\) från den negativa plattan?
Lösning: Om du kallar spänningen \(U\) och avståndet mellan plattorna för \(s\) så gäller \(\displaystyle E = \frac{U}{s}\). Det andra uttrycket för fältstyrkan är \(\displaystyle E = \frac{F}{Q}\). Du kan då teckna ekvationen \[ \frac{F}{Q} = \frac{U}{s} \text{ eller } F = \frac{Q \cdot U}{s} = \frac{1{,}60 \cdot 10^{-19} \cdot 180 }{0{,}025} \text{ N} = 1{,}2 \cdot 10^{-15} \text{ N} \]
En pytteliten kraft? Ja kanske det, men för elektronen betyder det en enorm acceleration. Om den accelereras \(0{,}5 \text{ cm}\) mot den positiva plattan hinner den komma upp i en fart på \(3{,}6 \cdot 10^6 \text{ m/s}\). Det är \(1 \ \%\) av ljushastigheten! Med den farten skulle det ta \(11 \text{ s}\) runt jorden.
Spänningen mellan ett åskmoln och jorden kan vara \(200\) miljoner volt. Om blixten orsakar en urladdning på \(50 \text{ C}\), hur stor elektrisk energi frigörs då vid blixtnedslaget?
Lösning: Den frigjorda energin blir \[ W = QU = 50 \cdot 2 \cdot 10^8 \text{ J} = 1{,}0 \cdot 10^{10} \text{ J} \]
Energin i blixten kommer från snabbt uppåtstigande luftströmmar, och är alltså omvandlad solenergi. Vi kan inte utnyttja denna energi, men vackert är det. Elektriska spänningar kan egentligen uppstå var som helst och när som helst i naturen. Du har säkert fått en eller annan elektrisk stöt vid något tillfälle, till exempel när du tagit i en ledstång. Visste du förresten att det är elektriska impulser som via hjärnan styr alla dina rörelser. Det som händer är att det har skapats en elektrisk obalans genom att olika laddningar på något sätt har separerats. Det är samma princip oavsett om det gäller nervimpulser, åskmoln eller batterier. Så länge det finns en spänning kan elektronerna förflytta sig för att utjämna skillnaden i laddning.

