9 Elektricitet: 9.6 Koppling av motstånd
 Seriekoppling
Seriekoppling
9.6 Koppling av motstånd
Seriekoppling
Vi seriekopplar två motstånd med resistanserna \(R_1\) och \(R_2\). Se figur 9.23. Med en voltmeter mäter vi spänningarna \(U_1\) och \(U_2\) över vart och ett av de två motstånden och spänningen \(U\) över båda motstånden. Resultatet blir att \[ U = U_1 + U_2 \] Resultatet är inte oväntat, för spänningen \(U\) är ju ett mått för det arbete per laddningsenhet som behövs för att föra strömmen genom ett motstånd. När vi för en viss laddning genom två seriekopplade motstånd, måste vi ju utföra ett arbete \(W\) som är lika med summan \(W_1 + W_2\) av de arbeten som behövs för vart och ett av motstånden.

Spänningen över en seriekoppling av motstånd är lika med summan av spänningarna över vart och ett av motstånden \[ U = U_1 + U_2 + \ldots + U_n \]
Vi mäter också strömmen I genom de båda motstånden. Därefter ersätter vi de två motstånden med ett enda motstånd, så att strömmen \(I\) och spänningen \(U\) blir lika stora som tidigare. Resistansen i ett sådant motstånd kallar vi ersättningsresistansen i seriekopplingen.
En koppling av motstånd kan ersättas med ett enda motstånd. Resistansen i detta motstånd kallar vi ersättningsresistansen för kopplingen.
Spänningen \(U\) över seriekopplingen är \(U = RI\), där \(R\) är ersättningsresistansen. Spänningen över vart och ett av motstånden är \[ U_1 = R_1 I \text{ och } U_2 = R_2 I \]
Av formeln \(U = U_1 + U_2\) får vi \[ RI = R_1 I + R_2 I \]
Vi dividerar med \(I\) på bägge sidorna och får \[ R = R_1 + R_2 \] Vi får motsvarande resultat om vi seriekopplar fler än två motstånd.
Ersättningsresistansen i en seriekoppling är lika med summan av de enskilda resistanserna, \[ R = R_1 + R_2 + \ldots + R_n \] Formeln visar att ersättningsresistansen alltid är större än den största av de enskilda resistanserna i seriekopplingen.
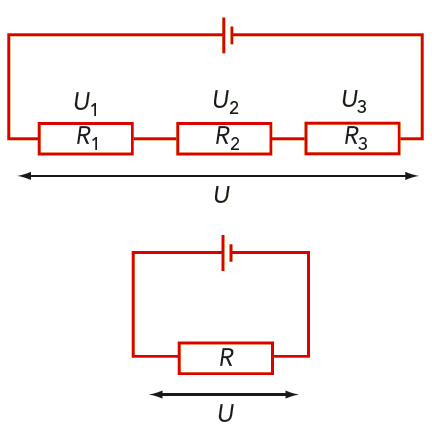
I en strömkrets finns tre seriekopplade motstånd, där \(R_1 = 2{,}0 \text{ Ω}\), \(R_2 = 3{,}0 \text{ Ω}\) och \(R_3 = 4{,}0 \text{ Ω}\). Se figur 9.24. Voltmetern visar att spänningen över hela seriekopplingen är \(4{,}5 \text{ V}\), och amperemetern visar att strömmen genom hela kretsen är \(0{,}50 \text{ A}\).
- Vad blir spänningen över de olika motstånden?
- Vad blir ersättningsresistansen?
Lösning:
- Spänningen över de olika motstånden blir: \[ U_1 = R_1 \cdot I = 2{,}0 \cdot 0{,}50 \text{ V} = 1{,}0 \text{ V} \] \[ U_2 = R_2 \cdot I = 3{,}0 \cdot 0{,}50 \text{ V} = 1{,}5 \text{ V} \] \[ U_3 = R_3 \cdot I = 4{,}0 \cdot 0{,}50 \text{ V} = 2{,}0 \text{ V} \] Summan blir \( U_1 + U_2 + U_3 = 4{,}5 \text{ V}\). Det är samma spänning som voltmetern visar.
- När vi löser uppgiften adderar vi de tre motstånden. Vi får ersättningsresistansen \[ R = R_1 + R_2 + R_3 = 2{,}0 \text{ Ω} + 3{,}0 \text{ Ω} + 4{,}0 \text{ Ω} = 9{,}0 \text{ Ω} \]

