9 Elektricitet: 9.7 Potential
 9.7 Potential
9.7 Potential
9.7 Potential
Som du vet har ett föremål potentiell energi i gravitationsfältet och man brukar ofta sätta den potentiella energin lika med noll, då föremålet befinner sig på jordytan.
Detta är jämförbart med förhållandena för en elektrisk laddning i ett elektriskt fält där laddningen i varje punkt har en potentiell elektrisk energi. Man har kommit överens om att sätta denna till noll, då laddningen befinner sig på jorden eller i en ledare som står i förbindelse med jorden.
I figur 9.31 har den undre plattan kopplats till jord och den potentiella energin är därför noll där.
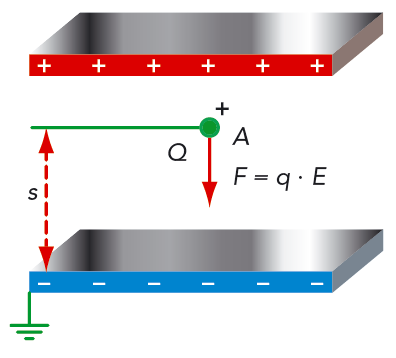
Laddningen \(Q\) befinner sig vid ett tillfälle på avståndet \(s\) från den undre plattan och har då en potentiell energi \(W_\text{p}\). För att föra laddningen från punkten A till den jordade plattan krävs att fältet utför ett elektriskt arbete. Detta arbete är lika stort som laddningens potentiella energi. \[ W = W_\text{p} = Fs = QEs \text{, men detta kan skrivas som } \frac{W_\text{p}}{Q} = Es \]
Tidigare har vi definierat elektrisk spänning som \[ U = W/Q \]
Uttrycket \[ \frac{W_\text{p}}{Q} \] anger således spänningen mellan punkten A och jord (den jordade plattan). Denna spänning kallas potential och betecknas \(V_\text{A}\).
Potentialen i en punkt A definieras som \( \displaystyle V_\text{A} = \frac{W}{Q} \) där \(W\) är fältets arbete då en positiv laddning \(Q\) förs från punkten A till jord.
Detta kan också definieras som spänningen mellan punkten och jord.
Enheten för potential är volt, \(\text{V}\).
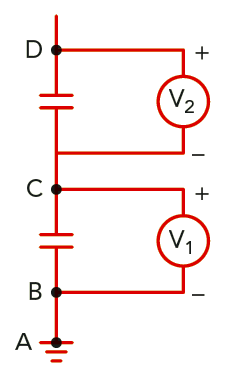
De två voltmetrarna i figuren visar \(V_1 = 3{,}0 \text{ V}\) och \(V_2 = 6{,}0 \text{ V}\). Bestäm potentialen i punkterna A, B, C och D.
Lösning: Punkterna A och B har potentialen \(0 \text{ V}\), eftersom båda är anslutna till jord.
Voltmetern \(V_1\) mäter spänningen mellan punkten C och jord. Då måste potentialen i C vara \(V_\text{C} = 3{,}0 \text{ V} \).
Spänningen mellan punkten D och jord är \((3{,}0 + 6{,}0) \text{ V} = 9{,}0 \text{ V}\). Potentialen i punkten D är således \(V_\text{D} = 9{,}0 \text{ V}\).
Av resonemanget ovan ser du att spänningen mellan två punkter är lika med potentialskillnaden mellan punkterna. \(V_\text{D} = 9{,}0 \text{ V}\) och \(V_\text{C} = 3{,}0 \text{ V}\). \(U = V_\text{D} - V_\text{C} = 6{,}0 \text{ V}\), vilket är precis det som voltmetern \(V_2\) visar.
Spänningen \(U\) mellan två punkter är lika med potentialskillnaden mellan punkterna. \[ U = V_2 - V_1 \]
Vi ska föra en positiv laddning från den undre plattan till den övre längs vägen A-B-C-D-E. Punkterna A och E ligger på plattorna. Beräkna potentialen i punkterna A-E.
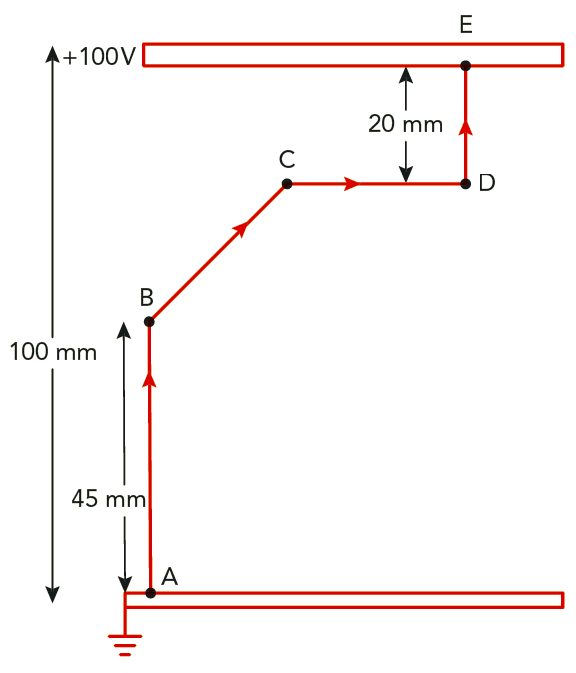
Lösning: Vi använder oss av sambandet \( \displaystyle V = \frac{W}{Q} = Es \), där \(\displaystyle E = \frac{U}{s}\).
Fältet är homogent och därför är fältstyrkan lika stor överallt. \[ E = \frac{U}{s} = \frac{100}{0{,}1} \text{ V/m} = 1000 \text{ V/m} \]
I punkten A är potentialen noll, \(V_\text{A} = 0 \text{ V}\), eftersom punkten befinner sig på den jordade plattan. Sträckan mellan A och B är \(0{,}045 \text{ m}\). Potentialen i punkten B blir \(V_\text{B} = Es = 1 \ 000 \cdot 0{,}045 \text{ V} = 45 \text{ V}\).
När laddningen når punkten C har den rört sig \(35 \text{ mm}\) mellan punkterna B och C längs fältlinjerna. Totala förflyttningen från punkten A längs fältlinjerna är \(80 \text{ mm}\). \(V_\text{C} = Es = 1 \ 000 \cdot 0{,}080 \text{ V} = 80 \text{ V}\)
\(V_\text{C} = V_\text{D} = 80 \text{ V}\) eftersom det inte krävs något arbete att föra laddningen från C till D. Laddningen befinner sig lika långt från plattan i båda punkterna.
I punkten E blir potentialen \( V_\text{E} = Es = 1 \ 000 \cdot 0{,}100 \text{ V} = 100 \text{ V} \) eftersom laddningen nu totalt har rört sig \(100 \text{ mm}\).

