9 Elektricitet: 9.8 Elektrisk energi och effekt
 9.8 Elektrisk energi och effekt
9.8 Elektrisk energi och effekt
9.8 Elektrisk energi och effekt
De elektriska laddningarna i en strömkrets tillförs energi i spänningskällan. När laddningarna passerar genom ett motstånd, förlorar de energi. Men energin bevaras, så vad händer med denna energi? Hemma har vi elektriska kokplattor, ugnar och lampor. I dessa fall ger strömmen en temperaturökning, och energin överförs till omgivningen som värme och ljus.
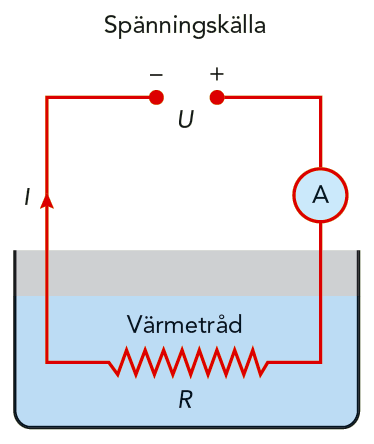
James Joule, som vi har mött i tidigare kapitel, studerade energiövergångar. Bland annat upptäckte han ett samband mellan elektrisk ström och elektrisk energi. Joule sänkte ned ett motstånd i en värmemätare med känd värmekapacitet. Se figur 9.36. Därefter skickade han en ström genom motståndet och mätte temperaturstegringen i värmemätaren. Det gick alltså värme från motståndet till värmemätaren.
Elektrisk effekt
Vi kan komma fram till ett uttryck för effekten i ett motstånd genom att utnyttja det vi lärt tidigare i detta kapitel:
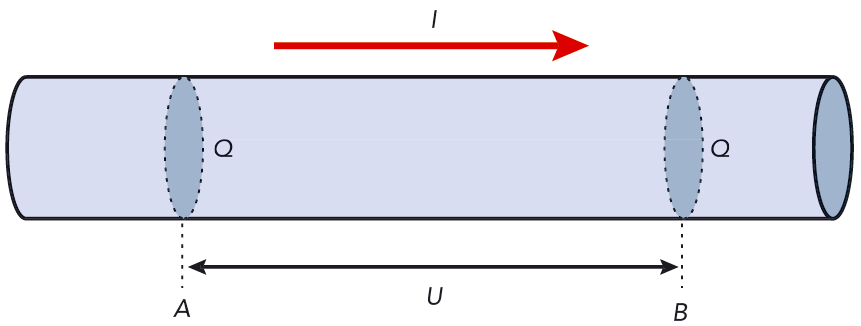
- Tänk dig en cylinderformad ledare av metall. Se figur 9.37.
- En elektrisk ström \(I\) går genom ledaren, och under tiden \(t\) går en laddning in genom ett tvärsnitt vid \(A\) och ut genom ett tvärsnitt vid \(B\).
- Det motsvarar att en laddning transporteras från \(A\) till \(B\). Spänningen mellan \(A\) och \(B\) är lika med \(U\).
- På laddningen \(Q\) utförs alltså ett arbete.
Effekten P kan beräknas: \[ P = \frac{W}{t} = \frac{QU}{t} = \frac{It \cdot U}{t} = U \cdot I \]
Arbetet \(W\) leder inte till att elektronerna i ledaren får högre kinetisk energi. Allt arbete omvandlas till termisk energi när ledningselektronerna kolliderar med metalljonerna.
Den elektriska effekten i ett motstånd är lika med spänningen över motståndet multiplicerad med strömmen genom motståndet, \[ \text{Effekt} = \text{spänning} \cdot \text{ström} \ \text{ eller } \ P = UI \]
eller omformulerat med Ohms lag \[ P = \frac{U^2}{R} \ \text{ eller } \ P = R \cdot I^2 \]
En kokplatta avger en effekt på \(1,5 \text{ kW}\). Nätspänningen är \(230 \text{ V}\). Hur stor är resistansen i motståndstråden?
Lösning: Av \( \displaystyle P = \frac{U^2}{R} \) får vi \[ R = \frac{U^2}{P} = \frac{230^2}{1500} \text{ Ω} = 35 \text{ Ω}\]

