9 Elektricitet: 9.3 Spänning
 Elementarladdningen
Elementarladdningen
Elementarladdningen
Elektronen upptäcktes i slutet av 1800-talet. På den tiden räknade fysikerna med att det måste finnas en elementarladdning, det vill säga en minsta elektrisk laddning. All elektrisk laddning måste då vara ett heltal gånger elementarladdningen. Under åren 1909 - 1913 utförde amerikanen Robert Millikan (1868 - 1953) en försöksserie för att försöka hitta den elektriska elementarladdningen.
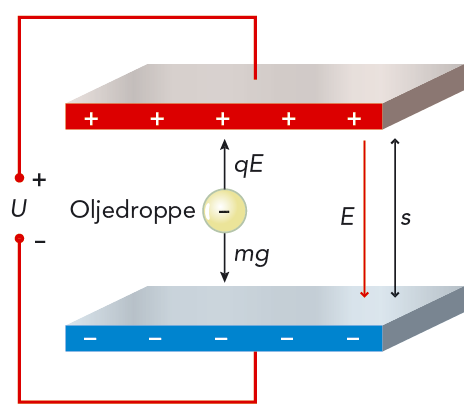
Millikan blåste in små oljedroppar i ett elektriskt fält mellan två horisontella metallplattor. Se figur 9.9. Några av dropparna blev elektriskt laddade, och de negativa dropparna påverkades av en elektrisk kraft som pekade lodrätt uppåt. Millikan justerade fältstyrkan så att en av dropparna stod stilla. Enligt Newtons första lag måste då den elektriska kraften på oljedroppen vara lika stor som droppens tyngd. Ur ekvationen \(qE = mg\) fick han laddningen \[ q = \frac{mg}{E} \]
Millikan studerade oljedroppen i mikroskop. Han mätte radien och beräknade droppens volym. När han kände oljans densitet, kunde han beräkna oljedroppens massa \(m\). Vidare mätte han spänningen \(U\) mellan metallplattorna och avståndet \(s\) mellan plattorna. Då kunde han beräkna den elektriska fältstyrkan \(E = U/s\) och därmed också laddningen \(q = mg/E\).
Försök med flera tusen oljedroppar visade att den negativa laddningen på dropparna alltid var lika med ett heltal gånger en bestämd minsta laddning \(e\). Laddningen \(q\) var alltså lika med \(e\), \(2e\), \(3e\) och så vidare.
En oljedroppe med massan \(m = 8{,}2 \cdot 10^{-16} \text{ kg}\) och negativa laddningen \(q\) är i vila mellan två parallella, horisontella metallplattor. Spänningen mellan plattorna är \(U = 150 \text{ V}\), och avståndet mellan plattorna är \(s = 6{,}0 \text{ mm}\). Den översta plattan är positiv. Den elektriska fältstyrkan har absolutvärdet \[ E = \frac{U}{s} = \frac{150}{6{,}0 \cdot 10^{-3}} \text{ V/m} = 2{,}5 \cdot 10^4 \text{ V/m} \]
När oljedroppen är i vila, är den elektriska kraften \(F = qE\) lika stor som tyngden \(Fg = mg\) men motsatt riktad. Laddningen på oljedroppen blir \[ q = \frac{mg}{E} = \frac{8{,}2 \cdot 10^{-16} \cdot 9{,}82 }{2{,}5 \cdot 10^4} \text{ C} = 3{,}2 \cdot 10^{-19} \text{ C} \]
Eftersom den elektriska kraften \(qE\) verkar uppåt, måste droppen ha den negativa laddningen \(-3{,}2 \cdot 10^{-19} \text{ C}\). Droppen har alltså ett överskott på två elektroner. Jämför detta överskott med antalet atomer i oljedroppen om vi antar att varje atom väger omkring \(10^{-26} \text{ kg}\).

