Resistansen i en metalltråd

9 Elektricitet: 9.5 Resistans

Resistansen i en metalltråd

Mätningarna som Ohm gjorde visade att en tjock tråd gav mindre motstånd än en tunn tråd som var lika lång eftersom det är lättare för laddningarna att ta sig fram i en tjockare tråd. En lång tråd gav större motstånd än en kort tråd som var lika tjock. Detta är också naturligt.

Resistivitet

Om man lägger samma spänning över en lång och en kort tråd blir det elektriska fältet lägre i den långa tråden. Detta medför att elektronernas driftshastighet och därmed strömmen blir lägre i den långa ledaren. Resistansen \(R\) i en metalltråd är alltså proportionell mot trådens längd \(l\), och omvänt proportionell mot trådens tvärsnittsarea \(A\).

Resistansen i en metalltråd kan vi skriva som \[ \text{Resistans} = \text{resistivitet} \cdot \frac{\text{trådens längd}}{\text{trådens area}} \ \text{ eller } \ R = \rho \cdot \frac{I}{A} \]

där \(\rho\) är en konstant som vi kallar resistiviteten hos metallen. Resistiviteten är karaktäristisk för metallen i tråden. Goda ledare har låg resistivitet.

Exempel 11

Högtalarkablar

9.19 Metaller har mycket låg resistivitet, de är ledare. Alla ämnen leder elektricitet om spänningen blir tillräckligt hög, men isolatorer kräver mycket hög spänning. Halvledare intar en mellanställning. De finns i nästan all modern elektronik.

Anta att du vill koppla in ett par extrahögtalare till din stereoanläggning. Vilken längd ska kopparkablarna ha om genomskärningsarean är \(1{,}5 \text{ mm\(^2\)}\) och resistansen högst ska vara \(0{,}1 \text{ Ω}\)?

Lösning: Ur tabellsamlingen får vi att resistiviteten för koppar är \[ 1{,}67 \cdot 10^{-2} \left(\frac{\text{Ω} \cdot \text{mm\(^2\)} }{\text{m}} \right) \]

Ur enheten för resistivitet ser du att längden ska vara i \(\text{m}\) och arean i \(\text{ mm\(^2\)}\).

Nu kan du använda sambandet \(\displaystyle R = \rho \cdot \frac{I}{A} \), som du kan skriva om till \(\displaystyle I = \frac{A \cdot R}{\rho} \). \[ I = \frac{1{,}5 \cdot 0{,}1}{1{,}67 \cdot 10^{-2}} \text{ m} = 8{,}98 \text{ m}\] Högtalarkablarna ska vara ungefär \(9 \text{ m}\) långa.

Exempel 12

Resistansen i en lampa

Om vi vill undersöka resistansen i en lampa, är det naturligt att göra några olika mätningar vid varierande spänningar och strömstyrkor. Se figur 9.20. Den vänstra grafen är en förstoring av den första lilla biten av grafen till höger. Vad kan det bero på att grafen till höger inte är linjär?

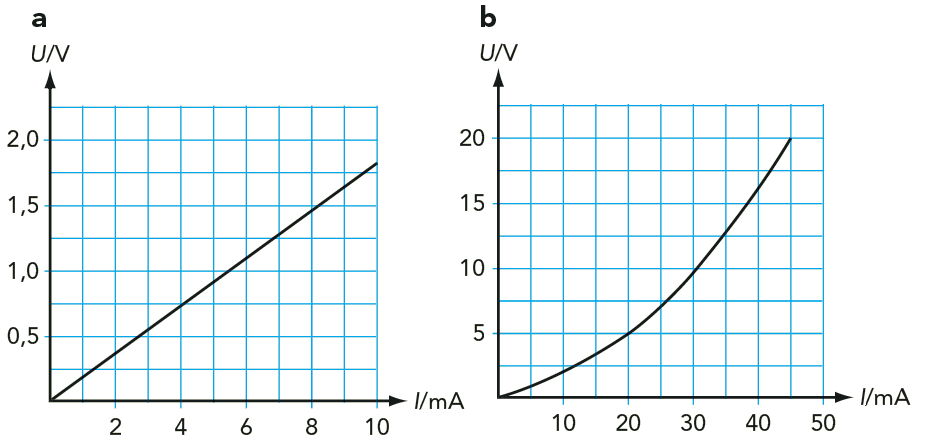
9.20 Graferna visar sambandet mellan ström och spänning för en glödlampa.

Bestäm glödtrådens resistans i figur a.
Bestäm glödtrådens resistans vid strömmen \(40 \text{ mA}\).

Lösning:

Resistansen får vi genom att beräkna \( \displaystyle R = \frac{U}{I} \). I figuren ser du att detta motsvarar linjens lutning. Om vi läser av grafen då \(I = 10 \text{ mA}\) får vi att \(U = 1{,}8 \text{ V}\). \[ R = \frac{U}{I} = \frac{1{,}8}{10 \cdot 10^{-3}} \text{ Ω} = 180 \text{ Ω} \]
I högra figuren ser du att spänningen ungefär är \(16 \text{ V}\) då strömmen är \(40 \text{ mA}\). \[ R = \frac{U}{I} = \frac{16}{40 \cdot 10^{-3}} \text{ Ω} = 400 \text{ Ω} \]

9.21

Temperaturen i glödtråden i lampan är mycket högre vid strömmen \(40 \text{ mA}\) i figur b, jämfört med figur a. Försök visar att resistansen i en metallisk ledare ökar när temperaturen ökar. Det har att göra med att ju högre temperaturen är, desto kraftigare svänger metallatomerna runt sina jämviktslägen, och desto svårare blir det för elektronerna att passera genom ledaren. En enkel jämförelse: Det är svårare för en hund att springa genom en orolig folkmassa än att springa genom en grupp soldater som står uppställda på led.