9 Elektricitet: 9.6 Koppling av motstånd
 Parallellkoppling
Parallellkoppling
Parallellkoppling
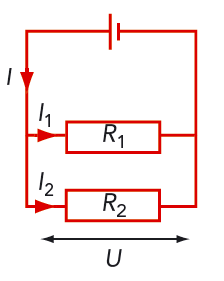
Vi parallellkopplar två motstånd med resistanserna \(R_1\) och \(R_2\). Se figur 9.25. Strömmen genom vart och ett av de två motstånden kallar vi grenström, och strömmen till och från förgreningspunkterna kallar vi för kretsens huvudström. Det går in lika mycket laddning till en förgreningspunkt som det går ut från den. Det är ungefär som med bilar i en vägkorsning. Lika många bilar som kommer in i korsningen kommer ut ur den.
Huvudströmmen i en parallellkoppling är lika med summan av grenströmmarna.
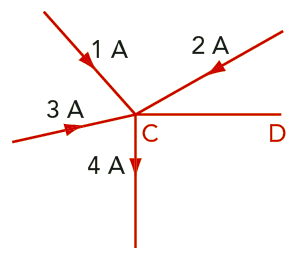
Ange strömmens storlek och riktning i ledaren CD i figuren.
Lösning: Som du ser är 6 A på väg in mot punkten C och 4 A på väg ut från samma punkt. Eftersom ingen ström samlas i någon punkt måste ytterligare 2 A vara på väg ut från punkten C. Svaret blir således att 2 A är på väg från punkten C mot punkten D.
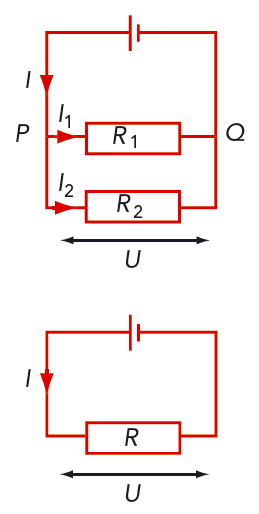
Vi kan ersätta de två motstånden i figur 9.27 med ett enda motstånd utan att huvudströmmen \(I\) och spänningen \(U\) ändras. Resistansen \(R\) i ett sådant motstånd är ersättningsresistansen för parallellkopplingen. Spänningen över vart och ett av de två motstånden är lika med spänningen \(U\) mellan förgreningspunkterna \(P\) och \(Q\).
Grenströmmarna blir därför \[ I_1 = \frac{U}{R_1} \ \text{ och } \ I_2 = \frac{U}{R_2} \]
Huvudströmmen blir \(I = U/R\). Vi sätter in uttrycken för \(I\), \(I_1\) och \(I_2\) i strömförgreningslagen. Det ger \[ \frac{U}{R} = \frac{U}{R_1} + \frac{U}{R_2} \]
Vi dividerar med \(U\) på båda sidorna och får \[ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} \] Vi får motsvarande resultat om vi parallellkopplar fler än två motstånd.
Ersättningsresistansen för en parallellkoppling ges av formeln \[ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_n} \] Ersättningsresistansen för en parallellkoppling är alltid mindre än den minsta av de enskilda resistanserna i parallellkopplingen.

Vi har en strömkrets med två grenar. Se figur 9.28. Resistanserna är \(R_1 = 20 \text{ Ω}\) och \(R_2 = 30 \text{ Ω}\). Spänningen över parallellkopplingen är \(U = 12 \text{ V}\). Beräkna grenströmmarna och ersättningsresistansen för parallellkopplingen.
Lösning: Strömmen i de två grenarna får vi fram med Ohms lag. Vi får \[ I_1 = \frac{U}{R_1} = \frac{12}{20} \text{ A} = 0{,}60 \text{ A} \ \text{ och } \ I_2 = \frac{U}{R_2} = \frac{12}{30} \text{ A} = 0{,}40 \text{ A} \]
Enligt strömförgreningslagen är huvudströmmen \[ I = I_1 + I_2 = (0{,}60 + 0{,}40) \text{ A} = 1{,}00 \text{ A} \]
När vi känner spänningen och huvudströmmen, kan vi beräkna ersättningsresistansen genom att använda Ohms lag. Vi får \[ R = \frac{U}{I} = \frac{12}{1{,}00} \text{ Ω} = 12 \text{ Ω} \]
Alternativt kan vi beräkna ersättningsresistansen på följande sätt: \[ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} = \frac{1}{20} + \frac{1}{30} \]
\( R = 12 \text{ Ω} \) (Glöm inte att invertera)
Lägg märke till att ersättningsresistansen är mindre än den minsta av de enskilda resistanserna.

Figur 9.29 visar tre motstånd som är kopplade till en spänningskälla på \(12 \text{ V}\). Vi ska beräkna ersättningsresistansen i kretsen och strömmen genom det minsta motståndet.
Lösning: Motstånden är kopplade i en kombination av parallellkoppling och seriekoppling. Först beräknar vi ersättningsresistansen \(R_\text{par}\) för parallellkopplingen: \[ \frac{1}{R_\text{par}} = \frac{1}{R_1} + \frac{1}{R_2} = \frac{1}{15} + \frac{1}{30} \] \[ R_\text{par} = 10 \text{ Ω} \]
Ersättningsresistansen för hela kretsen blir därför \[ R = R_\text{par} + R_3 = 10 \text{ Ω} + 40 \text{ Ω} = 50 \text{ Ω} \]
Huvudströmmen i kretsen blir \[ I = \frac{U}{R} = \frac{12}{50} \text{ A} = 0{,}24 \text{ A} \]
Nu kan vi beräkna spänningen över parallellkopplingen, \[ U_\text{par} = R_\text{par} \cdot I = 10 \cdot 0{,}24 \text{ V} = 2{,}4 \text{ V} \]
Slutligen beräknar vi strömmen \(I_1\) genom det minsta motståndet: \[ I_1 = \frac{U_\text{par}}{R_1} = \frac{2{,}4}{15} \text{ A} = 0{,}16 \text{ A} \]
Lägg märke till att spänningen över parallellkopplingen inte är \(12 \text{ V}\), utan bara \(2{,}4 \text{ V}\). (Spänningen över motståndet på \(40 \text{ Ω} \) är \(9{,}6 \text{ V}\). Det kan du kontrollera på två sätt. Gör det!)

