9 Elektricitet: 9.7 Potential
 Kirchoffs lagar
Kirchoffs lagar
Kirchhoffs lagar
Vi ska nu ägna lite mer tid åt att undersöka elektriska kretsar med hjälp av potentialbegreppet. Strömförgreningslagen känner du redan till från avsnitt 9.6. Lagen kallas även Kirchhoffs första lag efter den tyske fysikern Gustav Kirchhoff (1824 – 1887). Vi ska nu komplettera med Kirchhoffs andra lag.
I varje sluten strömkrets är summan av alla potentialändringar lika med noll.
Om vi jämför med tyngdkraftfältet igen så blir det mycket tydligare vad den här lagen betyder. Tänk dig att du är ute i skogen och springer i en motionsslinga. Om du sätter utgångspunkten som nollnivå så ändras din potentiella energi varje gång du springer uppför eller nedför någon backe. Men när du kommer tillbaka till utgångspunkten igen så måste summan av alla dessa förändringar vara noll eftersom du är tillbaka på samma nivå som när du startade. På samma sätt är summan av alla potentialändringarna i en sluten krets lika med noll.
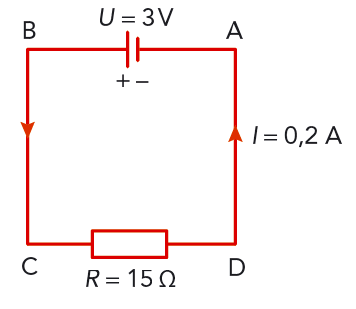
Den potentiella energin ökar när du springer uppför en backe, eftersom du arbetar i motsatt riktning som gravitationsfältet (som ju verkar nedåt) och din potentiella energi minskar då du springer nedför backe, eftersom du då arbetar i samma riktning som fältet. På samma sätt är det med elektrisk potential. Se figur 9.34. Det elektriska fältet i batteriet är riktat från pluspol till minuspol. Om vi går från A till B genom batteriet, mot fältriktningen, ökar potentialen. När vi däremot går från B till A genom motståndet går vi i samma riktning som fältet, det vill säga i strömmens riktning. Då sjunker potentialen med beloppet \(R \cdot I\). Om vi går ett varv moturs, A-B-C-D-A får vi enligt Kirchhoffs andra lag:
\[ U + ( - RI) = 0 \text{, det vill säga } \ 3 + ( - 15 \cdot 0{,}2) = 0. \text{ Stämmer!} \]
I en strömkälla stiger potentialen i riktning från den negativa polen till den positiva och sjunker åt andra hållet. För en resistor sjunker potentialen i strömriktningen och stiger i motsatt riktning.
En förstärkare i en musikanläggning måste drivas av både en negativ och en positiv spänning för att kunna ge rätt signal till högtalarna.
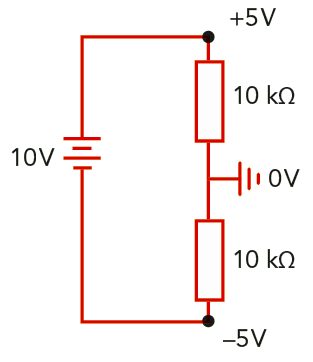
Rita en krets som består av en 10 volts likspänningskälla och två lika stora motstånd. Kretsen ska jordas på lämpligt ställe för att man skall få ut \( \ +/- 5 \text{ V}\).
Lösning: Bilden visar ett exempel på hur man skulle kunna göra. Man bygger en så kallad spänningsdelare (två motstånd kopplade serie som delar upp den pålagda spänningen i två delar) med de två motstånden och jordar mellan motstånden.
Vi har en seriekoppling, därför blir ersättningsresistansen \(20 \text{ kΩ}\). Strömmen blir \[ I = \frac{U}{R} = \frac{10}{20 \cdot 10^3} \text{ A} = 0{,}5 \text{ mA} \]
Låt oss nu gå från jord och uppåt i kretsen. Vi går mot fältet, potentialen ökar med \(R \cdot I = 10 \ 000 \cdot 0{,}5 \cdot 10^{-3} \text{ V} = 5 \text{ V}\). Beräkningarna blir desamma när vi går nedåt i kretsen men då går vi med fältet och därför minskar potentialen (till \(-5 \text{ V}\)).
Det är bra med stora motstånd eftersom man inte vill att det skall gå mycket ström genom spänningsdelaren.

