11 Kärnfysik: 11.5 Halveringstid
 11.5 Halveringstid
11.5 Halveringstid
11.5 Halveringstid
Rutherford gjorde försök som visade att radioaktivitet omvandlar ett grundämne till andra grundämnen. Det betyder att det efter hand blir mindre och mindre kvar av det radioaktiva ämnet. En viktig egenskap hos radioaktiva ämnen är halveringstiden \( T_{1/2}\).
Halveringstiden är den tid som förflyter innan hälften av alla atom kärnorna i ett radioaktivt ämne har omvandlats till andra atomkärnor.
Halveringstiden är en karakteristisk egenskap hos ett radioaktivt ämne och varierar kraftigt från ämne till ämne. Det finns radioaktiva ämnen med en halveringstid på \(10-9 \text{ s}\), medan till exempel uran har en halveringstid på \(7{,}5 \cdot 10^9\) år, lika lång som jordens ålder. Halveringstiden är oberoende av hur många atomkärnor det finns i ämnet från början.
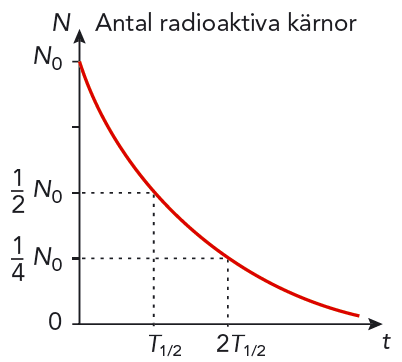
Om vi startar med \(N_0\) radioaktiva kärnor av ett ämne vid tiden \(t = 0\), så har vi kvar \( \frac{1}{2} N_0 \) kärnor av detta ämne efter tiden \(t = T_{1/2}\). De övriga kärnorna har omvandlats. Efter tiden \( t = 2T_{1/2} \) har hälften av de resterande \(\frac{1}{2} N_0 \) kärnorna omvandlats, och bara \(\frac{1}{4} N_0 \) av de ursprungliga kärnorna finns kvar. Efter ytterligare en halveringstid är andelen ursprungliga kärnor nere i \( \frac{1}{8} N_0 \) . Och så fortsätter det. Se figur 11.14.
Efter \(x\) halveringstider har antalet kärnor minskat till \[ N = N_0 \cdot \left( \frac{1}{2} \right)^x \]
Vid tiden \(t\) har det gått \( x = \left. t \right/ T_{1/2}\) halveringstider. Det ger oss:
I ett radioaktivt ämne minskar antalet radioaktiva atomkärnor med tiden. Om antalet är \(N_0\) vid tiden \(t = 0\), så har antalet vid tiden \(t\) reducerats till \[ N = N_0 \cdot \left( \frac{1}{2} \right)^{ \frac{t}{T_{1/2}} } \] där \( T_{1/2} \) är halveringstiden. \((N_0 - N)\) kärnor har omvandlats.
Vi har \(0{,}50\) milligram av det radioaktiva ämnet polonium-\(210\). Halveringstiden är \(138\) dygn. Hur mycket av ämnet finns kvar efter ett år?
Lösning: I sönderfallslagen kan vi räkna med ämnets massa på samma sätt som med antalet atomkärnor. Vi sätter \(t = 365\) dygn, \(T_{1/2} = 138\) dygn och \(m_0 = 0,50 \text{ mg}\). Massan \(m\) efter ett år blir då \[ m = m_0 \cdot \left( \frac{1}{2} \right)^{\frac{t}{T_{1/2}}} = 0{,}50 \cdot \left( \frac{1}{2} \right)^{\frac{365}{138}} \text{ mg} = 0{,}080 \text{ mg} \]
Luft innehåller koldioxid, \( \rm CO_2 \). I en bråkdel av \( \rm CO_2 \)-molekylerna är kolet radioaktivt, nämligen den del som innehåller \( \rm C\text{-}14 \). Radioaktivt kol, \( \rm C\text{-}14 \), har en halveringstid på \(5 \ 730\) år. I samma takt som \( \rm C\text{-}14 \) sönderfaller, skapar den kosmiska strålningen ny \( \rm C\text{-}14 \) i atmosfären. Bråkdelen \( \rm CO_2 \)-molekyler med \( \rm C\text{-}14 \) håller sig därför ungefär konstant i luften.
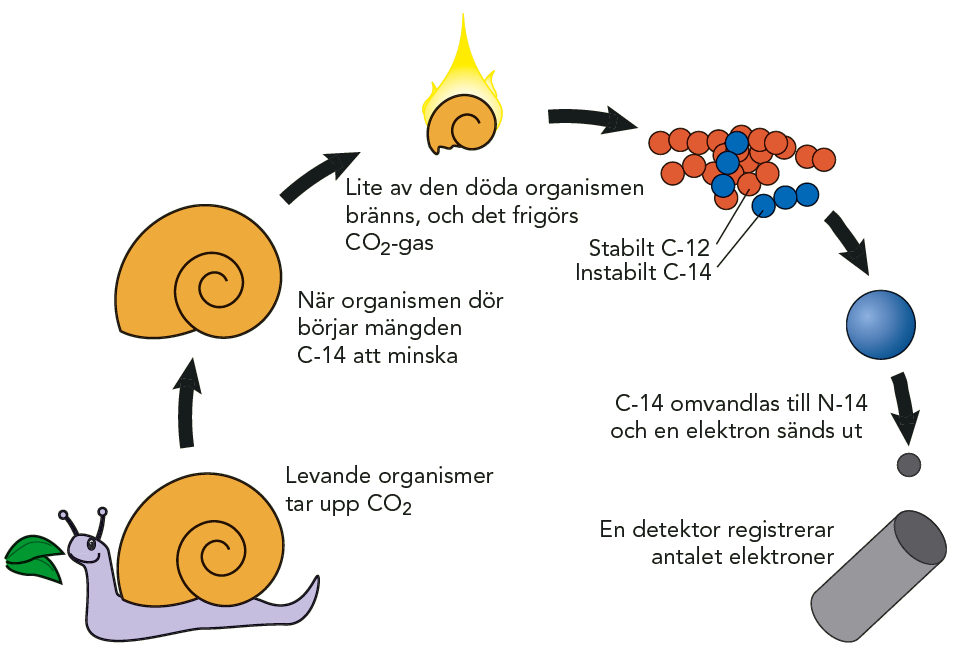
Växter tar upp \( \rm CO_2 \) från luften, djur äter växter, och människor äter både växter och djur. En konstant, liten bråkdel av kolet hos levande växter, djur och människor är därför radioaktivt \( \rm C\text{-}14 \). När växter eller djur dör, och inte längre tar upp nytt kol, börjar mängden \( \rm C\text{-}14 \) att minska. Se figur 11.15. Genom att mäta bråkdelen av \( \rm C\text{-}14 \) i rester från växt- eller djurriket kan arkeologerna beräkna hur gamla resterna är.
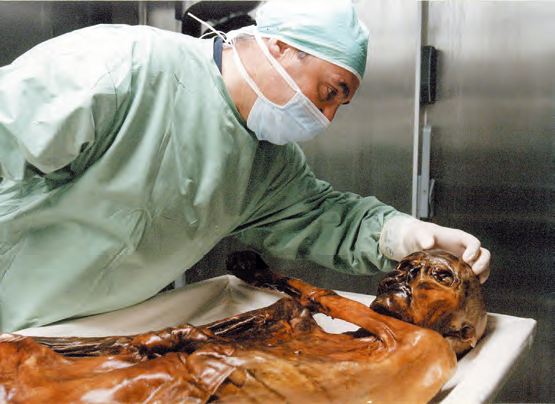
Om innehållet av \( \rm C\text{-}14 \) i en träbit eller en benrest är hälften av innehållet i levande material, räknar arkeologerna med att träbiten eller benresten är cirka \(5 \ 730\) år gammal. Om däremot halten \( \rm C\text{-}14 \) bara är blir åldern på föremålet dubbelt så stor, \(2 \cdot 5 \ 730 \text{ år} \approx 11 \ 500\). Under den varma sommaren 1991 smälte glaciärerna i Alperna mer än de hade gjort på mycket länge. I september befann sig ett turistande tyskt par lite utanför den vanliga vandringsleden i Ötztalalperna på gränsen mellan Italien och Österrike. De upptäckte då ett lik från en man som smält fram ur isen. Den mycket välbevarade kroppen som låg infrusen på över \(3 \ 000 \text{ m}\) höjd hade före infrysningen mumifierats av vind och sol. Både hud, naglar och hår hade bevarats. Man hittade även skor, kläder av skinn och en hel del redskap. Man har gjort flera olika \( \rm C\text{-}14 \) mätningar och kommit fram till att fyndets ålder är ungefär \(5 \ 300\) år gammalt. Ötzi eller ismannen som fyndet också kallas är den hittills äldsta bevarade människokroppen.
När sönderfaller en viss radioaktiv atom? Det kan vi inte veta. Sönderfallet sker av sig själv. Ingen kan påverka en atom till att sönder falla, och ingen kan förutsäga när en viss atom ska sönderfalla. Det vi kan förutsäga är, att under loppet av en halveringstid kommer ungefär hälften av atomerna att sönderfalla. Vi vet däremot inte vilka atomer som kommer att sönderfalla.

