11 Kärnfysik: 11.6 Fission av tunga kärnor
 11.6 Fission av tunga kärnor
11.6 Fission av tunga kärnor
11.6 Fission av tunga kärnor

År 1938 lyckades den tyske kemisten Otto Hahn att klyva den sällsynta uranisotopen \( \ce { ^{235}_{92} $ \rm U$} \) genom att skjuta långsamma neutroner mot urankärnan. Att långsamma neutroner med liten kinetisk energi kunde klyva en atom kärna, verkade helt otroligt. Han kontaktade sin medarbetare, den österrikiska fysikern Lise Meitner, och bad henne förklara fenomenet. På kort tid lyckades hon förklara uranfissionen teoretiskt. Hahn och Meitner skrev en rapport om upptäckten, som väckte uppseende bland fysiker världen över. Tyvärr fick Otto Hahn ensam nobelpriset för upptäckten, något som på senare år har blivit mycket omdebatterat.
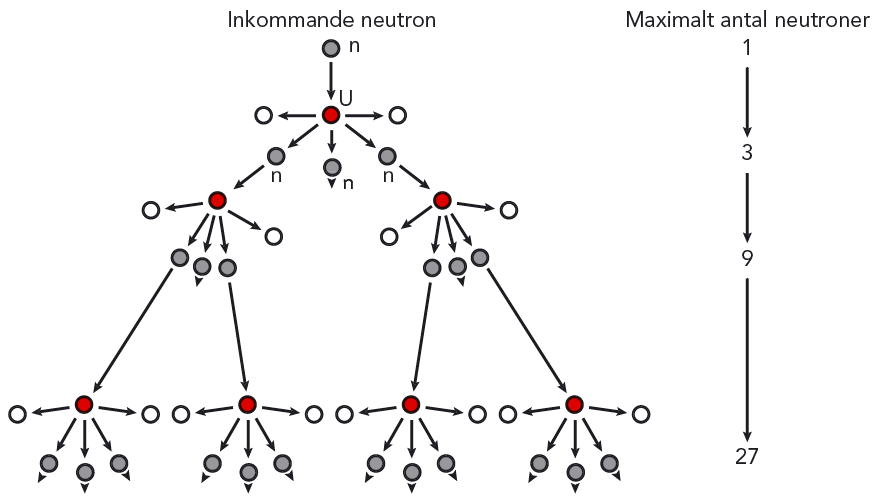
Det mest uppseendeväckande var den stora energimängd som frigjordes vid fissionen. Om det dessutom frigjordes ytterligare neutroner vid klyvningen, så kunde de frigjorda neutronerna klyva ännu fler urankärnor, som i sin tur skulle sända ut neutroner, och så vidare. Då skulle det bli en kedjereaktion. Om så var fallet, så kunde uranfissionen frigöra enorma energimängder.
Svaret lät inte vänta på sig. När en långsam neutron tränger in i uran kärnan, \( \ce { ^{235}_{92} $ \rm U$} \), kan kärnan dela sig i två delar A och B som tillsammans har 92 protoner. Samtidigt utsänds två eller tre neutroner. En kedjereaktion var möjlig. Se figur 11.19.
Men för att kedjereaktionen verkligen ska äga rum måste uranstycket utgöra en kritisk massa. De frigjorda neutronerna går i genomsnitt ett stycke innan de klyver nästa kärna. Om uranstycket är för litet kommer de flesta neutronerna att passera ut ur stycket innan de har hunnit klyva en urankärna. Kritisk massa för ett sfäriskt stycke \( \ce { ^{235}_{92} $ \rm U$} \) är \(15 \text{kg} \). Med samma densitet som guld blir det mindre än en liter.
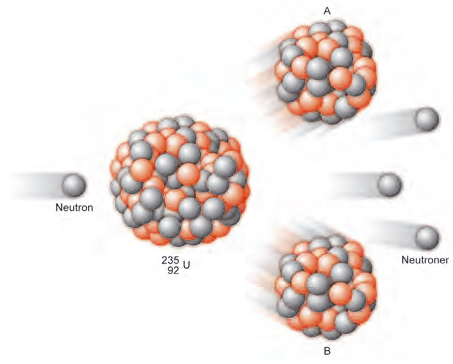
Urankärnan kan klyvas i två delar på ett antal olika sätt. Låt oss titta på ett av dem: \[ \ce { ^{235}_{92} $ \rm U$} + \ce { ^{1}_{0} $ \rm n$} \to \ce { ^{138}_{56} $ \rm Ba$} + \ce { ^{95}_{36} $ \rm Kr$} +3 \ \ce { ^{1}_{0} $ \rm n$} \]
En neutron tränger in i urankärnan, och det uppstår en mellankärna. Mellankärnan är mycket instabil och delar sig i två delar som stöter bort varandra med elektriska krafter. Delarna far därför iväg bort från varandra med stor kinetisk energi. Beräkna hur mycket energi som frigörs för varje urankärna som klyvs.
Lösning: Vi börjar med att ta reda på hur stora massorna är. \[ \ce { ^{235}_{92} $ \rm U$} \quad (m = 235{,}043923 \text{ u}) \] \[ \ce { ^{138}_{56} $ \rm Ba$} \quad (m = 137{,}905247 \text{ u}) \] \[ \ce { ^{95}_{36} $ \rm Kr$} \quad (m = 94{,}939711 \text{ u}) \] och till sist neutronens massa \[ (m_\text{n} = 1,008665 \text{ u}) \]
Total massa före sönderfallet:
\( (235{,}043923 + 1{,}008665) \text{ u} = 236,052588 \text{ u} \)
Total massa efter sönderfallet:
\((137{,}905247 + 94{,}939711 + 3 \cdot 1{,}008665) \text{ u} = 235{,}870953 \text{ u}\).
\[ \Delta m = (236{,}052588 - 235{,}870953) \text{ u} = 0{,}181635 \text{ u} \]
Den frigjorda energin blir \[ \Delta E = \Delta mc^2 = 0{,}181635 \cdot 1{,}66 \cdot 10^{-27} \cdot (3{,}00 \cdot 10^8)^2 \text{ J} = 2{,}7 \cdot 10^{-11} \text{ J} \] För varje urankärna som klyvs, frigörs totalt \( 2{,}7 \cdot 10^{-11} \text{ J} \). En urankärna kan klyvas på mer än \(300\) olika sätt, och det kan därför skapas mer än \(600\) olika dotterkärnor som alla är radioaktiva.

