11 Kärnfysik: 11.2 Krafter och energi i atomkärnan
 Bindningsenergi
Bindningsenergi
Bindningsenergi
Vi skulle kunna likna atomkärnan vid en energibrunn. Se figur 11.2. Nere i brunnen är nukleonerna bundna. I exemplet i figuren behövs det \(720 \text{ fJ}\) för att frigöra en nukleon. Det är nukleonens bindningsenergi.
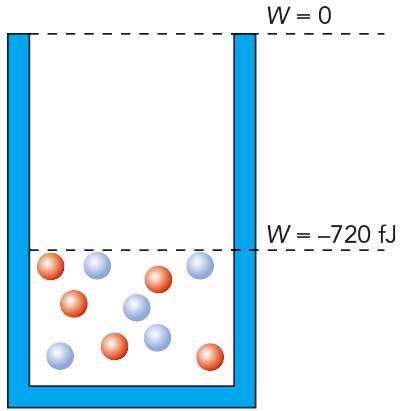
Den minsta energi som är nödvändig för att frigöra en nukleon från en atomkärna kallas nukleonens bindningsenergi.
Den minsta energi som är nödvändig för att frigöra en elektron från en atom, kallas atomens jonisationsenergi.
Precis som atomen skickade ut en foton då den gick från ett tillstånd till ett annat med lägre energi kan man tänka sig att det sker på liknande sätt vid en kärnreaktion. Tänk dig att en kärna fångar in en nukleon och att denna därefter "faller" ned i brunnen. Då sänder kärnan ut en foton med energin \(720 \text{ fJ}\). Skillnaden är att bindningsenergin är ungefär en miljon gånger större än jonisationsenergin. Detta är en typisk skillnad i storleksordning mellan atomenergier och kärnenergier.
Tänk dig en elektron som flyttas mellan två punkter som har en potentialskillnad på \(1\) volt. Elektronens laddning är \(e = 1{,}602 \cdot 10^{-19} \text{ J}\)
Vi känner till sambandet \(\displaystyle U = \frac{W}{Q} \), som kan skrivas som \(W = Q \cdot U\).
Energin som går åt för att flytta elektronen mellan de två punkterna är \[ W = Q \cdot U = e \cdot 1 \text{ V} = 1{,}602 \cdot 10^{-19} \text{ J} \] I atom- och kärnfysik är det vanligt att använda denna energi som enhet.
Denna energi kallas för \(1\) elektronvolt, \(1 \text{ eV} = 1{,}602 \cdot 10^{-19} \text{ J}\). Lägg märke till att elektronvolt är en energienhet och inte en enhet för spänning.
Den energi som går åt för att flytta en elektron mellan två punkter som har en potentialskillnad på \(1\) volt kallas \(1\) elektron volt (\(1 \text{ eV}\)).
Varje atom och varje specifik isotop har sina unika energier, sitt eget "fingeravtryck".
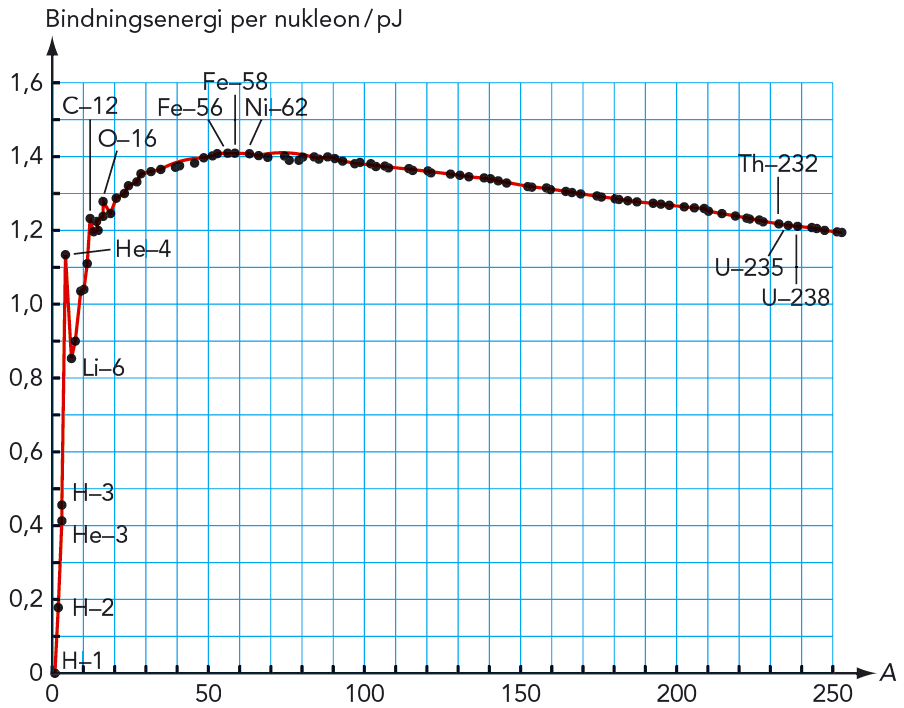
Vi kan också titta på den totala bindningsenergin för en kärna. Det är den energi som krävs för att frigöra alla nukleonerna, så att vi får ett antal fria protoner och neutroner. Om vi tar totala bindningsenergin och dividerar med antalet nukleoner får vi den genomsnittliga bindningsenergin per nukleon för just denna atomkärna. Figur 11.3 visar den genomsnittliga bindningsenergin per nukleon som funktion av nukleontalet för olika atomkärnor.