11 Kärnfysik: 11.4 Mer om radioaktivitet
 Alfastrålning (α-strålning)
Alfastrålning (α-strålning)
Alfastrålning ( \( \alpha \)-strålning)
En radioaktiv kärna av ett grundämne \( \rm X \) skickar ut en alfapartikel och omvandlas till en kärna av ett grundämne \( \rm Y\). Alfapartikeln är en heliumkärna, \( \ce { ^{4}_{2} $ \rm He$} \). Vi beskriver reaktionen på följande sätt: \[ \ce { ^{$A$}_{$Z$} $ \rm X $} \to \ce { ^{$A-4$}_{$Z-2$} $ \rm Y $} + \ce { ^{4}_{2} $ \rm He$} \]
När en atomkärna sänder ut en alfapartikel, sjunker protontalet med två enheter och masstalet med fyra enheter. Se figur 11.8. Andra exempel på alfastrålning är \[ \ce { ^{238}_{92} $ \rm U$} \to \ce { ^{234}_{90} $ \rm Th$} \to \ce { ^{4}_{2} $ \rm He$} \] \[ \ce { ^{222}_{86} $ \rm Rn$} \to \ce { ^{218}_{84} $ \rm Po$} \to \ce { ^{4}_{2} $ \rm He$} \]
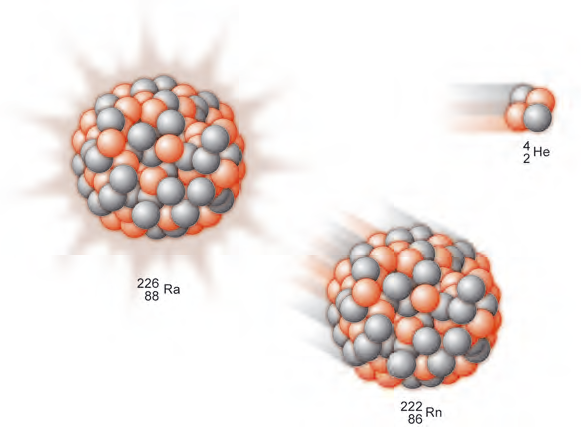
Den ursprungliga kärnan kallas moderkärna och kärnan som den sönder faller till kallas dotterkärna.
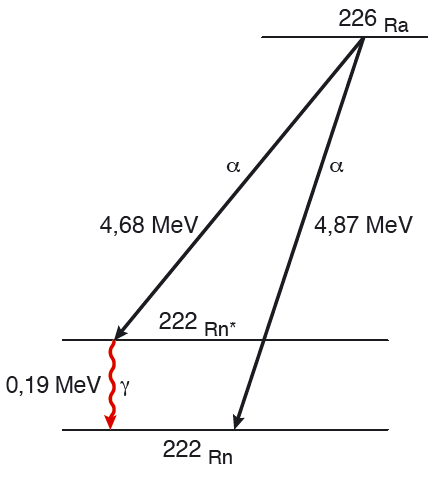
Beräkna hur mycket energi som frigörs när \( \ce { ^{226}_{88} $ \rm Ra$} \) \( (m = 226{,}025409 \text{ u}) \) sönderfaller till \( \ce { ^{222}_{86} $ \rm Rn$} \) \( ( m = 222{,}017576 \text{ u} ) \). Se figur 11.8.
Alfapartikeln, \( \ce { ^{4}_{2} $ \rm He$} \), har massan \( m = 4{,}0026033 \text{ u}\)
Lösning: Reaktionen kan skrivas \( \ce { ^{226}_{88} $ \rm Ra$} \to \ce { ^{222}_{86} $ \rm Rn$} + \ce { ^{4}_{2} $ \rm He$} \).
Total massa före sönderfallet: \(226{,}025409 \text{ u}\)
Total massa efter sönderfallet: \[ 222{,}017576 \text{ u} + 4{,}002603 \text{ u} = 226{,}020179 \text{ u} \] \[ \Delta m = 226{,}025409 \text{ u} - 226{,}020179 \text{ u} = 0{,}005230 \text{ u} \]
Eftersom \(1 \text{ u} = 931{,}49 \text{ MeV}\) så har det frigjorts \[ 0,005230 \cdot 931{,}49 \text{ MeV} = 4{,}87 \text{ MeV} \]
Alfapartiklar som sänds ut från en viss typ av atomkärnor, har bestämda kinetiska energier. Dotterkärnan är ofta exciterad och sänder ut ett eller flera gammakvanta. Se figur 11.9.
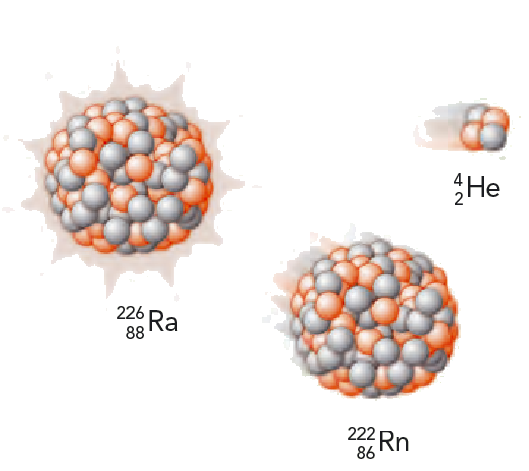
En radiumkärna \( \rm Ra\text{-}226\) sänder ut en alfapartikel och omvandlas till radonkärnan \( \rm Rn\text{-}222\), \[ \ce { ^{226}_{88} $ \rm Ra$} \to \ce { ^{222}_{86} $ \rm Rn$} + \ce { ^{4}_{2} $ \rm He$} \] Se figur 11.10. Alfapartikeln får hastigheten \(1,5 \cdot 10^7 \text{ m/s}\). Vi tänker oss att radiumkärnan var i vila före kärnreaktionen, och ska beräkna radonkärnans hastighet efter reaktionen.
Lösning: Rörelsemängden bevaras. Före reaktionen är rörelsemängden lika med noll. Därför måste rörelsemängderna vara lika med noll även efter reaktionen. Alltså blir \[ m_1 u_1 + m_2 u_2 = 0\] där \(m_1 = 222 \text{ u}\) är radonkärnans massa och \(m_2 = 4{,}0 \text{ u}\) är alfapartikelns massa. Radonkärnans hastighet blir \[ u_1 = \frac{m_2 u_2}{m_1} = - \frac{4{,}0 \cdot 1{,}5 \cdot 10^7 }{222} \text{ m/s} = -2{,}7 \cdot 10^5 \text{ m/s} \] Radonkärnan får alltså hastigheten \(270 \text{ km/s}\) i motsatt riktning mot alfapartikeln.

