11 Kärnfysik: 11.4 Mer om radioaktivitet
 Betastrålning (β-strålning)
Betastrålning (β-strålning)
Betastrålning (\(\beta\)-strålning)
En radioaktiv kärna av ett grundämne \( \rm X\) skickar ut en elektron och omvandlas till en kärna av ett annat grundämne \(Y\). Från början beskrev fysikerna reaktionen på följande sätt: \[ \ce { ^{$A$}_{$Z$} $ \rm X $} \to \ce { ^{$A$}_{$Z+1$} $ \rm Y $} + \ce { ^{0}_{-1} $ \rm e $} \] Lägg märke till sättet att beteckna elektronen. Talet \(0\) visar att elektronen inte är en nukleon, och talet \(-1\) visar att laddningen är en negativ elementarladdning.
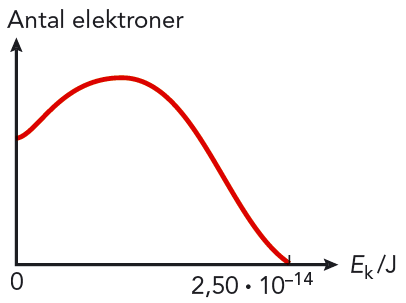
Ursprungligen ansåg fysikerna att betastrålningen bara innehöll elektroner. Till exempel skulle en reaktion kunna se ut så här: \[ \ce { ^{14}_{6} $ \rm C$} \to \ce { ^{14}_{7} $ \rm N$} + \ce { ^{0}_{-1} $ \rm e$} \] Här borde elektronen komma ut med samma kinetiska energi, från alla \( \ce { ^{14}_{6} $ \rm C$} \)-kärnor. Man beräknade energin till \(2,50 \cdot 10-14 \text{ J}\). Men mätningar visade att elektronerna kom ut med en energi som varierade mellan \(0\) och \(2{,}50 \cdot 10^{-14} \text{ J}\). Se figur 11.11. Det kunde se ut som om totalenergin inte bevarades vid betastrålning.
Lösningen kom med en märklig partikel som heter antineutrino, \( \bar \nu \). Den saknar laddning och har nästan ingen massa. Antineutrinon är därför mycket svår att påvisa. Tillsammans för elektronen och antineutrinon med sig energin \(2,50 \cdot 10^{-14} J\) vid varje omvandling av \( \ce { ^{14}_{6} $ \rm C$} \)-kärnor. Det som varierar, är det sätt på vilket de två partiklarna fördelar energin. Om elektronen tar liten kinetisk energi, så får antineutrinon stor energi, och tvärt om. Antineutrinon påvisades första gången år 1956.
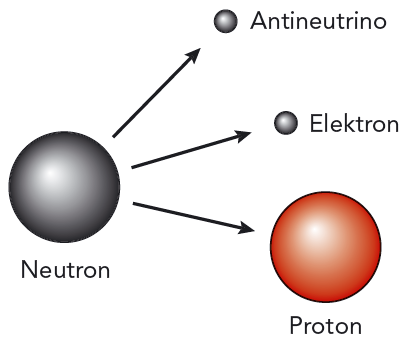
a) En neutron omvandlas till en proton, en elektron och en antineutrino. Denna process frigör energi.
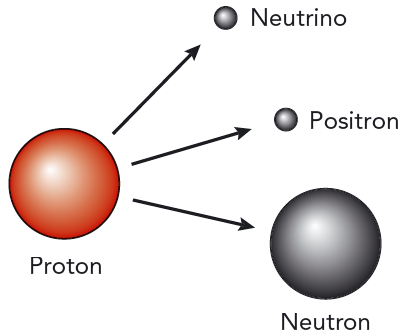
b) En proton omvandlas till en neutron, en positron och en neutrino. Denna process kräver energi.
Elektronerna i betastrålning kommer från atomkärnorna, men kärnorna innehåller ju inte elektroner! Det måste betyda att elektronerna skapas vid själva omvandlingen. Reaktionsformlerna visar att nukleontalet är oförändrat, medan protontalet ökar med 1. Den nya kärnan har fått en proton mer och en neutron mindre än den gamla kärnan. Vi tänker oss därför att en neutron omvandlas till en proton, samtidigt som det skapas en elektron och en antineutrino: \[ \ce { ^{1}_{0} $ \rm n$} \to \ce { ^{1}_{1} $ \rm p$} + \ce { ^{0}_{-1} $ \rm e$} + \bar \nu \] Denna reaktion går av sig själv, eftersom neutronen har större massa än protonen. Se figur 11.12a.
Vi kan nu skriva den fullständiga reaktionen för \( \beta \)-sönderfall på följande sätt: \[ \ce { ^{$A$}_{$Z$} $ \rm X$} = \ce { ^{A}_{Z+1} $ \rm Y $} + \ce { ^{0}_{-1} $ \rm e$} + \bar \nu \]
Följande reaktioner är exempel på betastrålning: \[ \ce { ^{14}_{6} $ \rm C$} \to \ce { ^{14}_{7} $ \rm N$} + \ce { ^{0}_{-1} $ \rm e$} + \bar \nu \] \[ \ce { ^{234}_{90} $ \rm Th$} \to \ce { ^{234}_{91} $ \rm Pa$} + \ce { ^{0}_{-1} $ \rm e$} + \bar \nu \]
År 1934 lyckades Irène och Frédéric Joliot-Curie skapa konstgjorda radioaktiva isotoper. Vissa av dem sände ut en annan typ av betastrålning, nämligen en positron och en neutrino \( \nu\). Ett exempel är följande reaktion \[ \ce { ^{11}_{6} $ \rm C$} \to \ce { ^{11}_{5} $ \rm B$} + \ce { ^{0}_{1} $ \rm e$} + \nu \]
Positronen är en så kallad antipartikel (även antineutrino är en antipartikel). Den liknar på alla sätt en positiv elektron, men om en elektron och en positron möts, förintas båda i en blixt av gammastrålning. Positronen har samma massa som elektronen, men motsatt laddning. Vi räknar med att positronen blir till i kärnan på följande sätt: \[ \ce { ^{1}_{1} $ \rm p$} \to \ce { ^{1}_{0} $ \rm n$}+\ce { ^{0}_{1} $ \rm e$} + \nu \] Se figur 11.12 b. Denna process kräver energi.
För att kunna skilja mellan de olika \(\beta\)-sönderfallen brukar de kallas \(\beta-\) respektive \(\beta+\).
Beräkna hur mycket energi som frigörs när \( \ce { ^{14}_{6} $ \rm C$} \) \( ( 14{,}003242 \text{ u} ) \) sönderfaller till \( \ce { ^{14}_{7} $ \rm N$} \) \( ( 14,003074 \text{ u} )\) med ett \(\beta\)-sönderfall.
Lösning: Reaktionen kan skrivas \( \ce { ^{14}_{6} $ \rm C$} \to \ce { ^{14}_{7} $ \rm N$} + \ce { ^{0}_{-1} $ \rm e$} + \bar \nu \)
Här måste vi se upp eftersom nuklidmassorna är hela den neutrala atomens massa. Detta innebär massan av kärnan och alla elektronerna.
Kolkärnan är med sina sex elektroner en neutral atom. Däremot är inte kväveatomen neutral eftersom det finns \(7\) protoner men bara \(6\) elektroner. Vi har alltså en positiv kvävejon efter sönderfallet. Massan efter sönderfallet beräknar vi på följande sätt: \[ \underbrace{ m ( \ce { ^{14}_{7} $ \rm N$} ) - m( \ce { ^{0}_{1} $ \rm e$} )}_{\text{kvävejonens massa}} + \underbrace{m ( \ce { ^{0}_{1} $ \rm e$} )}_{\text{\(\beta\)-partikelns massa}} = m ( \ce { ^{14}_{7} $ \rm N$} ) \] (inklusive \(7\) elektroner)
Total massa före sönderfallet: \(14{,}003242 \text{ u}\)
Total massa efter sönderfallet: \(14,003074 \text{ u}\)
\(\Delta m = 14{,}003242 - 14{,}003074 = 0{,}000168 \text{ u}\)
Det har frigjorts \(0{,}000168 \cdot 931{,}49 \text{ MeV} = 0{,}156 \text{ MeV}\).
Energin blir rörelseenergi som kommer att fördela sig mellan betapartikeln och antineutrinon. Dotterkärnans rörelseenergi blir försumbart liten eftersom den är ungefär \(25 \ 000\) gånger tyngre än elektronen.
Skriv reaktionsformeln när \( \ \ce { ^{23}_{12} $ \rm Mg$} \ \) sönderfaller med ett positronsönderfall.
Lösning: Reaktionen kan skrivas \( \ \ce { ^{23}_{12} $ \rm Mg$} + \ce { ^{23}_{11} $ \rm Na$} + \ce { ^{0}_{+1} $ \rm e$} + \nu \)

