11 Kärnfysik: 11.5 Halveringstid
 Aktivitet
Aktivitet
Aktivitet
Aktiviteten för ett radioaktivt ämne är ett mått på hur snabbt ämnet kommer att sönderfalla.
Aktiviteten för ett radioaktivt ämne är antalet sönderfall per tidsenhet i ämnet.
Symbolen för aktivitet är \(A\), och enheten är becquerel, Bq, \(1 \text{ Bq} = 1 \text{ s\(^{-1}\)}\). En becquerel är lika med ett sönderfall per sekund. En äldre enhet för aktivitet, som fortfarande används, är curie (\(\text{Ci}\)). Enheten är uppkallad efter Marie och Pierre Curie. \[ 1 \text{ Ci} = 3{,}7 \cdot 10^{10} \text{ Bq} \] vilket motsvarar aktiviteten hos \(1 \text{ g}\) radium.
Aktiviteten är proportionell mot antalet radioaktiva atomkärnor i ämnet, \(A = \text{konst} \cdot N\). Om vi kombinerar detta med sönderfallslagen \[ N = N_0 \cdot \left( \frac{1}{2} \right)^{ \frac{t}{T_{1/2}} } \] får vi aktivitetslagen:
I ett radioaktivt ämne minskar aktiviteten med tiden. Eftersom aktiviteten är \(A_0\) vid tiden \(t = 0\), har aktiviteten i ämnet vid tiden \(t\) minskat till \[ A = A_0 \cdot \left( \frac{1}{2} \right)^{ \frac{t}{T_{1/2}} } \] där \( T_{1/2} \) är halveringstiden för ämnet.
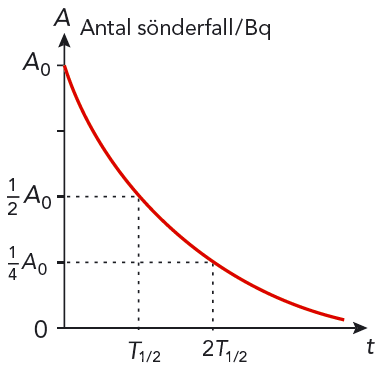
Se figur 11.17 och jämför med figur 11.14.
En gammakälla för skolbruk har aktiviteten \(370 \text{ kBq}\) när källan är ny. Källan innehåller cesium \(\rm Cs\text{-}137\) som har halveringstiden \(30\) år. Aktiviteten minskar med tiden. Efter \(10\) år har aktiviteten sjunkit till \[ A =A_0 \cdot \left(\frac{1}{2}\right)^{\frac{t}{T_{1/2}}} =370 \cdot \left( \frac{1}{2} \right)^{ \frac{10}{30} } \text{ kBq} = 294 \text{ kBq} \]
En avfallsbehållare från ett kärnkraftverk innehåller plutonium \(\rm Pu\text{-}239\) som har halveringstiden \(24 \ 400\) år. Hur lång tid måste förflyta innan aktiviteten har sjunkit till en tiondel?
Lösning: Vi sätter in \(A = 0{,}10 \cdot A_0\) i aktivitetsformeln och beräknar \(x = \left. t \right/ T_{1/2}\). \[ A = A_0 \cdot \left( \frac{1}{2} \right)^x \] \[ 0{,}10 \cdot A_0 = A_0 \cdot \left( \frac{1}{2} \right)^x \] \[ 0{,}10 = 0{,}50^x \] \[ x = \frac{\rm lg \ 0{,}10}{\rm lg \ 0{,}50} = 3{,}32 \]
Aktiviteten sjunker alltså till en tiondel på \(3{,}32\) halveringstider. Detta resultat gäller generellt. För \(\rm Pu\text{-}239\) blir tiden \[ t = x \cdot T_{1/2} = 3{,}32 \cdot 24 \ 400 \text{ år} \approx 81 \ 000 \text{ år} \]

