12 Relativitetsteori och standardmodell: 12.1 Relativitetsteori
 Einsteins revolution
Einsteins revolution
Einsteins revolution
I mitten av 1800-talet hade man experimentellt funnit att ljushastigheten \(c\) var ungefär \(300 000 \text{ km/s}\). Vid den här tiden hade man också kommit långt i utforskandet av elektriska och magnetiska fenomen. 1861 lyckades engelsmannen Maxwell (1831–1879) sammanfatta allt man visste om elektricitet och magnetism i några matematiska ekvationer. Ekvationerna visade att elektricitet och magnetism inte var separata fenomen utan olika sidor av elektromagnetismen. Maxwell lyckades även visa att man skulle kunna producera elektromagnetiska vågor. De här vågorna skulle enligt hans beräkningar ha en fart på \(300 000 \text{ km/s}\). Samma fart som ljuset! Men då måste väl ljus vara elektromagnetiska vågor? Den hypotesen bekräftades snabbt genom försök.
På den här tiden tänkte man att de elektromagnetiska vågorna måste ha ett medium som svängde med vågorna, som vatten med vattenvågor eller luft med ljudvågor. Man antog att det fanns ett sådant medium, etern, och att rymden var fyllt med det. Man kunde ju se solen och stjärnorna!
De elektromagnetiska vågorna antogs ha farten \(300 000 \text{ km/s}\) i förhållande till etern, ungefär som ljudvågor har farten \(340 \text{ m/s}\) i förhållande till luften. Då borde man även kunna mäta olika ljusfarter beroende på vår fart i förhållande till etern, precis som vi på en båt skulle mäta olika våghastigheter relativt båten beroende på båtens hastighet i förhållande till vattnet.
1887 påbörjade två forskare, Michelson och Morley, en serie försök för att ta reda på om ljushastigheten i förhållande till jorden var olika i olika riktningar.
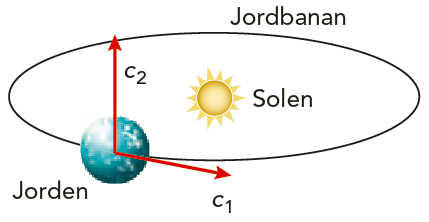
Figur 12.3 visar principen för försöket. Ljushastigheten mäts i en riktning längs jordbanan och i en riktning tvärs emot jordbanan. Vi kallar de två hastigheterna för \(c_1\) och \(c_2\). De flesta fysiker på den tiden ansåg att \(c_1\) och \(c_2\) inte kunde vara lika. Det skulle vara en naturlig konsekvens av att jorden rörde sig genom etern och att ljusets hastighet var konstant i förhållande till etern.
Resultatet blev inte det alla förväntade. Tvärtom, det uppseendeväckande resultatet blev att hur noga de än mätte, och vid vilken årstid de än gjorde det, så var ljusets hastighet parallellt med jordens bana runt solen, \(c_1\), exakt densamma som ljusets hastighet vinkelrätt mot jordens bana runt solen, \(c_2\).
Ytterst märkligt tyckte alla fysiker, utom den unge Albert Einstein (1879–1955), som konstaterade att det var precis det han förväntade sig. För om man räknade ut ljushastigheten utifrån experiment med elektricitet och magnetism på rymdskeppet Jorden, eller fann den direkt genom mäta hur lång tid det tar ljuset att tillryggalägga en viss sträcka, så borde man alltid få samma resultat.
Med utgångspunkt i den idén postulerade Einstein helt enkelt att ljushastigheten är densamma för alla observatörer, oavsett vilken fart de har. Det spelar ingen roll för mätresultatet om observatören är i vila eller i rörelse i förhållande till ljuskällan.
1905 publicerade Einstein den speciella relativitetsteorin. Teorin bygger på två postulat:
Mätningar av ljusets hastighet i vakuum ger samma resultat, \(c\), i alla referenssystem. Detta gäller oavsett med vilken fart observatören rör sig relativt ljuskällan. Vi kan inte förändra vår fart relativt ljuset.
Fysikens lagar förblir desamma i alla fritt fallande referenssystem. Ett exempel på ett fritt fallande referenssystem är en raket med frånslagna motorer.
Låt oss ta ett par steg i sällskap med Einstein och hans samtida och se vart Einsteins postulat för oss
Vi befinner oss på rymdfarkosten Jorden som dras med solen i ett svindlande fall runt Vintergatan. Einsteins omvälvande insikt var att vi alltid har samma fart \(c\) i förhållande till ljuset, oberoende av vår egen rörelse. Vi kan aldrig förändra vår fart i förhållande till ljuset!
Så måste det vara om naturlagarna är desamma för alla observatörer som seglar genom rymden i en raket med frånslagna motorer — som vi på rymdskeppet jorden. Annars skulle vi ju ha kunnat undersöka hur naturlagarna såg ut på just vår rymdfarkost, och använda resultatet som "hastighetsmätare".
Betrakta två rymdskepp. Ett som rör sig med farten \(0{,}5c\) i förhållande till ett annat. En ljusstråle jagar förbi de två rymdskeppen.
I det första rymdskeppet mäter man tiden som ljusstrålen använder för att passera rymdskeppet. Genom att dela sträckan med tiden, finner de att ljusstrålen rör sig med hastigheten \(c\) i förhållande till sitt rymdskepp.
Så passerar samma ljusstråle det andra rymdskeppet. De mäter också tiden det tar för ljusstrålen att passera sitt rymdskepp. De kommer fram till att ljusstrålen har hastigheten c i förhållande till sitt rymdskepp.
Samma ljusstråle har alltså hastigheten \(c\) i förhållande till två rymdskepp som har en enorm hastighet i förhållande till varandra.

Det låter som en paradox! Einsteins stora bedrift var att inse följande: eftersom ljushastigheten var densamma för alla observatörer som rör sig med konstant hastighet relativt varandra, kan observatörerna inte vara överens om sträckor och tidsintervall, det vill säga om tid och rum. Det ska vi strax förklara närmare.

