12 Relativitetsteori och standardmodell: 12.1 Relativitetsteori
 Tidsförlängning
Tidsförlängning
Tidsförlängning
Tänk dig nu att vi betraktar en ”ljusklocka” i tågvagnen i exempel 4. En ljusklocka fungerar så att den sänder en ljuspuls från taket i tåget rakt ner till en detektor på golvet. Ljusklockan mäter tiden det tar för ljuspulsen att ta sig från taket till golvet. Inget konstigt med det. Låt oss kalla den tiden, mätt inne i tåget för \(t_0\).
Föreställ dig nu att ljusklockan ombord på tåget betraktas av observatören på banvallen. Han ser tåget passera förbi med farten \(v\) åt höger. Han konstaterar att ljuset sändes ned och träffar detektorn på golvet. Men, under tiden som ljuset är på väg, rör sig tåget framåt med farten \(v\). Ljuspulsen måste därför gå snett nedåt. Hur skulle den annars ha kunnat träffa detektorn som flyttar sig med tågets fart medan ljuset är på väg?
Men om båda är överens om ljuspulsens hastighet och höjden i tågvagnen, då kan de inte vara överens om tiden det tog. Sett från banvallen hade ljuset längre väg – och det måste ta längre tid. Låt oss kalla den tiden för \(t\).
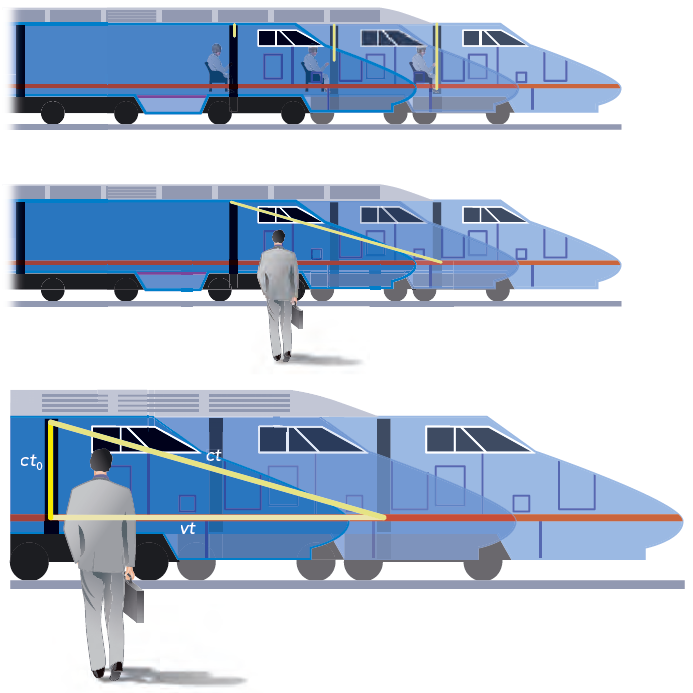
Nu kan vi använda Pythagoras sats för att få fram sambandet mellan den tid \(t_0\) som ljuspulsen använder från taket till golvet sett från tåget, och den tid \(t\) som ljuspulsen använder sett från banvallen: \[ (ct)^2 = (ct_0)^2 + (vt)^2 \] \[ (ct)^2 - (vt)^2 = (ct_0)^2 \] \[ t^2(c^2 - v^2) = (ct_0)^2 \] \[ t^2 = \frac{ (ct_0)^2 }{c^2 - v^2} = \frac{ t_0^2}{1 -\frac{v^2}{c^2} }\] \[ t = \frac{t_0}{\sqrt{1-\frac{v^2}{c^2}} } \] Nu har vi kommit fram till en mycket viktig relation som är den så kallade tidsförlängningen eller tidsdilatationen:
En klocka som rör sig med hastigheten v förbi en observatör som befinner sig i vila saktar sig i jämförelse med observatörens klocka enligt sambandet: \[ t = \frac{t_0}{\sqrt{1 - \frac{v^2}{c^2}} } \] \(t_0\) är den tid som den förbifarande klockan mäter upp när den stationära klockan mäter tiden \(t\).

Sambandet gäller alla typer av klockor, pendelur, pulsslag, atomklockor, kemiska reaktioner osv. Det gäller alla klockor eftersom det djupast sett handlar om den tid de mäter.
Nåja, tänker du, detta är exotisk och kanske rentav hypotetisk fysik. Men så är det inte. Denna märkliga relation bekräftas tusenfalt varje dag på laboratorier runt om i världen - och av dig själv när du använder GPS. Det är en liten effekt vid "normala" hastigheter, men dagens precisionsklockor kan ändå mäta den direkt när den ena klockan rör sig i joggingfart förbi den andra. Detta är alltså inte en osäker hypotes utan tvärtom en mursten i fysikens fundament.
Formeln blir mycket enklare om vi inför gammafaktorn, \( \displaystyle \gamma = \frac{1}{ \sqrt{1 - \frac{v^2}{c^2} } } \), då kan vi skriva \[ t = \gamma t_0 \]
\[ \gamma = \frac{1}{ \sqrt{1 - \frac{v^2}{c^2}} } \] där \(\gamma \ge 1\) för alla hastigheter \(v\). Likhet gäller bara om \(v = 0\).
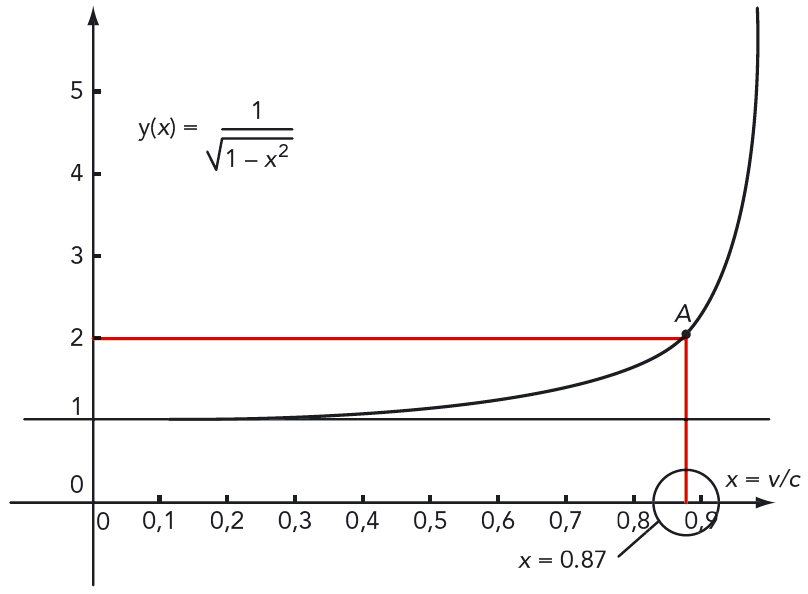
I vår bok räknar vi relativistiskt när hastigheten överstiger \(0{,}1c\), dvs. \(10 \text{ %}\) av ljushastigheten. Då är gammafaktorn \(\gamma = 1{,}0050\).
Vid "vanliga" hastigheter är gammafaktorn mycket nära \(1\).
När vi betraktar en klocka i rörelse relativt oss visar det sig alltså att den visar en annan tid än vår egen klocka. Men hur blir det med vår uppfattning av rummet?
En måttstock flyger förbi med farten \(v\). Gammafaktorn säger oss med vilken faktor längden i färdriktningen förkortas i förhållande till en måttstock i vila. \[ I = I_0 \cdot \sqrt{1 - \frac{v^2}{c^2}} \text{ eller } I = \frac{I_0}{\gamma} \]
Längden \(l_0\) i färdriktningen observeras av en som följer med den förbiflygande måttstocken. Längden \(l\) observeras av någon som ser måttstocken flyga förbi med farten \(v\).
Uttrycket kallas för längdförkortning, längdkontraktion eller Lorenzkontraktion. Lägg märke till att \(l \le l_0\) och att likhet bara gäller när observatörerna är vila i förhållande till varandra. Om en meterstav far förbi oss med farten \(v = 0,87c\) mäter vi den till en halv meter enligt grafen i figur 12.8.

