12 Relativitetsteori och standardmodell: 12.1 Relativitetsteori
 Energi i relativitetsteorin
Energi i relativitetsteorin
Energi i relativitetsteorin
Vi använder beteckningen \(E\), när vi pratar om relativistisk energi i stället för \(W\).
Kommer du ihåg att vi räknade ut den kinetiska energin hos ett föremål när vi utförde ett arbete på det. Vi fann att \( W_\text{k} = F \cdot s = \frac{1}{2}mv^2 \). Vi sade också att det var nästan sant. När farten blir så stor att vi måste räkna relativistiskt får vi ett helt annat uttryck.
Kraften är ju lika med massa gånger acceleration, och accelerationen beror av längd och tid som båda förändras när vi räknar relativistiskt. Både kraften \(F\) och vägen \(s\) kommer att ge relativistiska bidrag. Själva uträkningen kräver matematik som du inte lär dig förrän om ett par år, så vi skriver bara upp resultatet:
\[ E_\text{k} = \frac{mc^2}{\sqrt{1 - \frac{v^2}{c^2} } } - mc^2 \] eller på ett lite enklare sätt med gammafaktorn: \[ E_\text{k} = mc^2(\gamma -1) \]
Vi påstod även att det relativistiska uttrycket alltid är sant, det vill säga även vid låga farter, medan det klassiska uttrycket är nästan sant vid låga farter, men blir mer och mer fel vid högre farter. När farten överstiger \(0{,}1c\) brukar vi räkna relativistiskt här i gymnasiekursen.
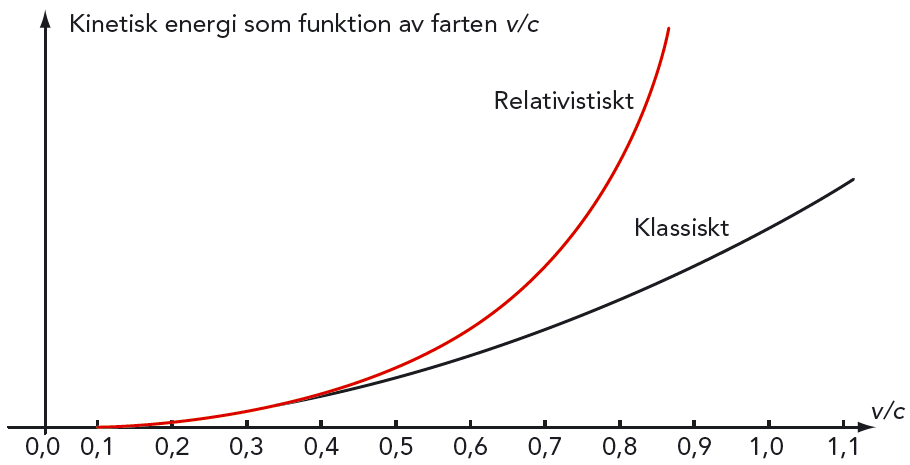
Men om båda uttrycken fungerar vid låga farter ska de ju ge ungefär samma resultat. Låt oss se på figur 12.9, som visar hur de två uttrycken utvecklar sig när farten ökar.
Som du ser stiger det klassiska uttrycket som en parabel förbi hastighets begränsningen, \(c\). Den relativistiska kinetiska energin däremot växer över alla gränser under tiden som farten närmar sig — men når aldrig fram till \(c\).
Inte ens om vi kunde använda vintergatans \(200\) miljarder stjärnors samlade effekt på en enda elektron kunde vi pressa upp den i ljusfarten. Men vi skulle komma mycket nära. På partikellaboratoriet CERN accelererar man just nu protoner upp till \(99{,}999999 \text{ %}\) av ljushastigheten.
När vi ser på uttrycket \(E_\text{kin} = \gamma mc^2 - mc^2\) så kan man ju undra över det andra ledet, \(mc^2\). Einstein insåg att \(\gamma mc^2\) var den totala energin som föremålet hade, och mc^2 var en energi det hade när det var i vila. Hur ska det tolkas?
Jo, det betyder att massa är ekvivalent med energi. Har vi massa så kan vi omforma den till energi och tvärtom. Det är det man håller på med på CERN. Man låter partiklar frontalkollidera så att summan av deras massenergier och rörelseenergier kan omvandlas till nya partiklar. Ju mer energi i kollisionen desto tyngre partiklar kan de producera. Alla kemiska eller kärnfysikaliska reaktioner som avger energi (exoterma) tar lite massa från bränslet. Till exempel en brinnande tändsticka. Väger man allt som kommer ut ur reaktionen så ser man att det är lite lättare än allt det som gick in i den.

När vi ser stjärnor lysa på natthimlen så är det massa som har omformats till elektromagnetisk energi som träffar våra ögon efter hundratals år i ljusets hastighet genom rymden. Det är alltså sådan massenergi som ger solen energin som strålar ut i alla riktningar, varav en pytteliten del driver hela det jordiska ekosystemet — som vi är en del av. Solen förlorar \(4{,}2 \cdot 10^9 \text{ kg}\) per sekund på sin energiproduktion. Som tur är så kan den fortsätta med det i ett par miljarder år till — men inte så mycket mer.
Sammanfattningsvis kan vi slå fast att ett föremåls totala energi är summan av dess kinetiska energi och dess viloenergi, när vi bortser från eventuell potentiell energi:
\[ E_\text{total} = \gamma mc^2 \text{, där } \gamma = \frac{1}{\sqrt{1- \frac{v^2}{c^2}} } \] Summan av kinetisk energi och massenergi mätt av en observatör som ser föremålet fara förbi med farten \(v\).
Hur stor är viloenergin i en sockerbit på \(5\) gram? Kontrollera att \(E_\text{vila} = mc^2\) ger svaret \(4{,}5 \cdot 10^{14}\) Joule. Men hur mycket energi är det? Bensin innehåller \(34{,}8 \text{ MJ/l}\) så det motsvarar \(13\) miljoner liter bensin. Tänk dig ett kubiskt rum med sida \(23{,}5\) meter fyllt med bensin!
Nu finns det bara en känd fysikalisk process som omformar precis all massenergi till ren energi och det är när partiklar möter antipartiklar så att båda förintas i gammastrålning. Men ingen har lyckats tänka ut hur en sådan energikälla ska tämjas, eftersom gammastrålningen blixtrar ut i alla riktningar, rätt igenom alla väggar. En sådan energikälla i en bil skulle döda alla i närheten utan att bilen flyttade sig en centimeter.

