3 Rörelse: 3.1 Medelhastighet
 3.1 Medelhastighet
3.1 Medelhastighet
3.1 Medelhastighet

Studera bild 3.1 här ovanför. \( 15 \) elever står uppställda längs en rät linje med två meters mellanrum. De sätter alla igång sina klockor samtidigt och var och en stoppar sin egen klocka då cyklisten Andreas passerar dem. Eleverna gör försöket två gånger och den andra gången håller Andreas en något högre hastighet. Båda gångerna gör han sitt bästa för att hålla en jämn hastighet. Mätresultaten ser du i tabellen nedan.
| Långsamt | Snabbt | ||
|---|---|---|---|
| \(t\)/s | \(t\)/s | \(s\)/m | |
| Jonas | \(0,00\) | \(0,00\) | \(0\) |
| Jonatan | \(0,62\) | \(0,37\) | \(2\) |
| Oscar | \(1,09\) | \(0,83\) | \(4\) |
| Linnea | \(1,63\) | \(1,35\) | \(6\) |
| Nikolina | \(2,36\) | \(1,78\) | \(8\) |
| Hanna | \(2,90\) | \(2,20\) | \(10\) |
| Martina | \(3,38\) | \(2,52\) | \(12\) |
| Malin | \(3,95\) | \(2,95\) | \(14\) |
| Lina | \(4,66\) | \(3,48\) | \(16\) |
| Simone | \(5,06\) | \(3,93\) | \(18\) |
| Jenny | \(5,65\) | \(4,23\) | \(20\) |
| Charlotte | \(6,35\) | \(4,62\) | \(22\) |
| Sandra | \(6,80\) | \(5,14\) | \(24\) |
| Peter | \(7,48\) | \(5,65\) | \(26\) |
| Emma | \(7,92\) | \(5,99\) | \(28\) |
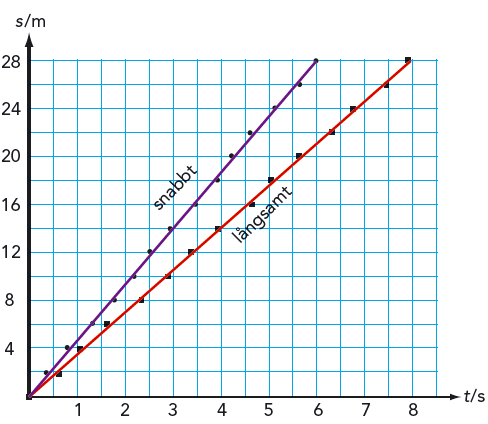
Sträckan \(s\) och tiden \(t\) är variabla storheter. Vi kan därför beskriva Andreas cykeltur grafiskt genom att pricka in värdena i ett diagram med \(t\) längs den vågräta axeln och \(s\) längs den lodräta axeln. Då får vi en \(s\)-\(t\)-graf. Figur 3.2 visar \(s\)-\(t\)-grafen för Andreas cykeltur.
Grafen kan vi nu använda för att ta reda på något om Andreas medelhastighet. Om du förflyttar dig sträckan \(s\) på tiden \(t\), så beräknar du medelhastigheten \(\bar v\) genom att dividera sträckan med tiden. Strecket över \(v\) betyder medelhastighet.
Medelhastighet är lika med sträcka dividerad med tid, \[ \text{Medelhastighet} = \frac{\text{sträcka}}{\text{tid}} \ \text{ eller } \bar{v} = \frac{s}{t} \] SI-enheten för hastighet är meter per sekund, \(\text{m/s}\).
Om vi nu skulle försöka beräkna de båda hastigheterna som Andreas cyklar med så bör vi försöka läsa av grafen så noggrant som möjligt. Låt oss börja med den långsammare cyklingen, som är den nedre av de två graferna. Där ser det ut som om Andreas hunnit ungefär \(28\) m på \(7{,}9\) s. Medelhastigheten får vi genom att dividera sträckan \(s\) med tiden \(t\). \[ \bar{v} = \frac{s}{t} = \frac{28}{7{,} 9} \text{ m/s} = {3{,}5} \text{ m/s} \]
Den andra medelhastigheten kan vi beräkna på liknande sätt. I diagrammet för den snabbare cykelturen kan vi se att Andreas har hunnit \(28 \text{ m}\) på ungefär \(6 \text{ s}\). \[ \bar{v} = \frac{s}{t} = \frac{28}{6} \text{ m/s} = {4{,}7} \text{ m/s} \]
Det här var ett enkelt exempel eftersom Andreas rör sig ungefär lika långt varje sekund. Lägg märke till att du enkelt kan jämföra hastigheter genom att titta i grafen. Ju fortare Andreas cyklar desto mer lutar grafen.
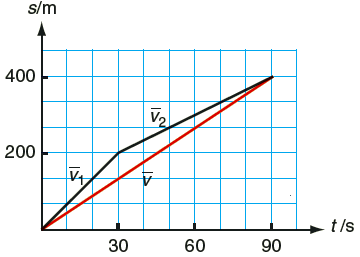
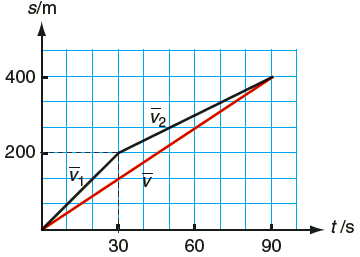
Lars är försenad till bussen som vanligt och konditionen är inte på topp. Han springer de första \(200\) m på \(30\) sekunder, sedan joggar han resterande \(200\) m på \(60\) sekunder. Totalt springer han \(400\) m på \(90\) sekunder. Medelhastigheten för hela loppet får vi genom att dividera hela sträckan med hela tiden. \[ \bar{v} = \frac{s}{t} = \frac{400}{90} \text{ m/s} = {4{,}4} \text{ m/s} \]
Under de första \(200\) metrarna är medelhastigheten \[ \bar{v_1} = \frac{s_1}{t_1} = \frac{200}{30} \text{ m/s} = {6{,}7} \text{ m/s} \]
Under de sista \(200\) metrarna är medelhastigheten \[ \bar{v_1} = \frac{s_1}{t_1} = \frac{200}{60} \text{ m/s} = {3{,}3} \text{ m/s} \]
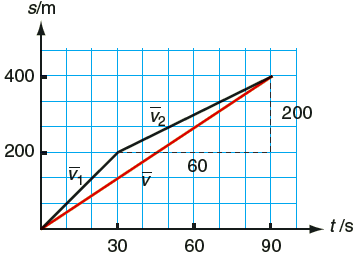
Lägg märke till att medelvärdet av \(\bar v_1\) och \(\bar v_2\) är \[ \frac{\bar{v_1} + \bar{v_2}}{2} = \frac{6{,}7}{3{,}3} \text{ m/s} = 5{,}0 \text{ m/s} \] och alltså inte lika med \(v = 4{,}4 \text{ m/s}\). För att beräkna medelhastigheten för hela loppet måste vi dividera hela sträckan med totala tiden.

