3 Rörelse: 3.3 Momentanhastighet
 3.3 Momentanhastighet
3.3 Momentanhastighet
3.3 Momentanhastighet
När hastigheten varierar kan man ändå ofta använda en modell med konstant hastighet. I den modellen är den konstanta hastigheten densamma som medelhastigheten. Men om du åker fast för fortkörning hjälper det inte så mycket att påstå att du har hållit hastighetsgränsen i genomsnitt. Låt oss därför se lite närmare på situationer där hastigheten varierar med tiden.
Hastighetsmätaren i bilar, cyklar och andra fordon visar ungefär hastigheten i varje ögonblick. Den kallas momentanhastighet. Du har säkert en känsla av vad det är som hastighetsmätaren visar, men begreppet momentanhastighet rymmer faktiskt svårigheter som det tog fysikerna århundraden att övervinna. Låt oss först titta på ett exempel.
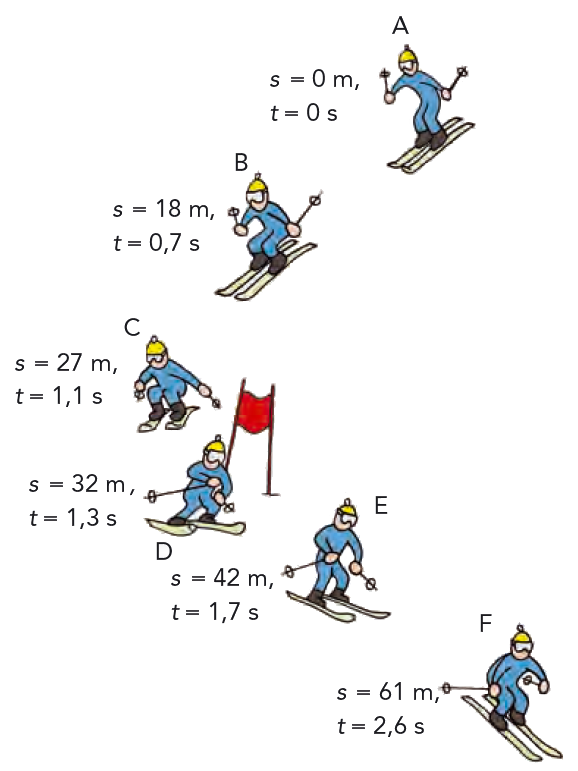
Hur skulle man kunna ta reda på vilken hastighet utförsåkaren har när han passerar flaggan? Se figur 3.9. Bildsekvensen visar sex ögonblicksbilder i hans utförsåk. Bilderna är gjorda så att flaggan ligger i mitten i alla tre fallen A \(\Rightarrow \) F, B \(\Rightarrow \) E och C \(\Rightarrow \) D. Med hjälp av avståndsmarkeringarna och klockan kan vi mäta både hur långt han har kört i de tre fallen och hur lång tid det har tagit. Ur detta kan vi beräkna åkarens medelhastighet \(\bar{v} = \Delta s / \Delta t\).
| \(\Delta s \ \) (m) | \(\Delta t \ \) (s) | \( \bar v \ \) (m/s) | |
|---|---|---|---|
| A \(\Rightarrow \) F | \( 61 \ (61 - 0) \) | \( 2{,}6 \ (2{,}6 - 0)\) | \(23{,}5\) |
| B \(\Rightarrow \) E | \(24 \ (42 - 18)\) | \(1{,}0 \ (1{,}7 - 0{,}7)\) | \(24{,}0\) |
| C \(\Rightarrow \) D | \(5 \ (32 - 27)\) | \(0{,}2 \ (1{,}3 - 1{,}1)\) | \(25{,}0\) |
Tecknet \( \Delta \) är den grekiska bokstaven delta, som motsvarar vårt D. Delta står för differens (skillnad) eller förändring. I detta sammanhang betyder \( \Delta s\) avståndet mellan två punkter, och \( \Delta t \) skillnaden mellan två tidpunkter.
Vi antar att v närmar sig ett bestämt värde ju kortare vi gör \( \Delta s \) och därmed \( \Delta t \). Utifrån mätningarna förväntar vi oss att detta värde ligger strax över \(25 \text{ m/s}\), kanske \(26 \text{ m/s}\)? I alla praktiska sammanhang när man talar om momentanhastigheten menar man medelhastigheten under ett "kort" tidsintervall. Lite slarvigt säger vi att åkarens momentanhastighet är \(25 \text{ m/s}\) när han passerar flaggan.
I praktiken kan man finna ett bra närmevärde för momentanhastigheten vid en tidpunkt \(t\), om man mäter medelhastigheten under ett tillräckligt kort tidsintervall omkring \(t\). Om hastigheten varierar mycket på kort tid, eller om man önskar stor noggrannhet kan sådana mätningar göras elektroniskt.
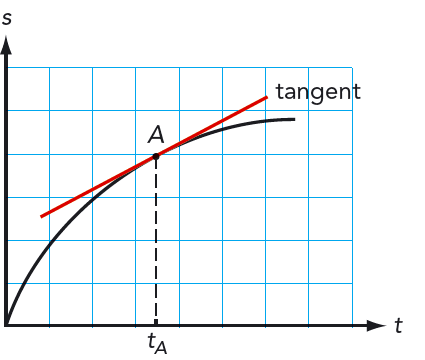
Ju fortare det går desto längre sträcka avverkas i varje tidsintervall. Det motsvarar en brantare \(s\)-\(t\)-graf. Se figur 3.10. Momentanhastigheten \(v\) vid en tidpunkt \(t\) motsvarar lutningen för tangenten i den aktuella punkten på \(s\)-\(t\)-grafen.


