3 Rörelse: 3.4 Acceleration
 Rörelseformlerna
Rörelseformlerna
Rörelseformlerna
Nu ska vi titta närmare på vår modell för acceleration. Vi förutsätter att accelerationen är konstant och vi kan då ställa oss frågan: hur kommer sambandet att se ut för motorcyklisten i exempel 3 om han har en hastighet \(v_0\) från början? Sambandet får då utseendet \[ v = v_0 + at \] på samma sätt som vid sträckformeln vid konstant hastighet. Detta är hastighetsformeln vid en accelererad rörelse.
När ett föremål har konstant acceleration, beräknas hastigheten v vid tidpunkten t som \[ v = v_0 + at \] där \( v_0 \) är starthastigheten.
Lägg märke till att det här är ekvationen för en rät linje som skär den lodräta axeln i punkten \( (0, v_0) \) och har lutningen \(a\). Se figur 3.15.
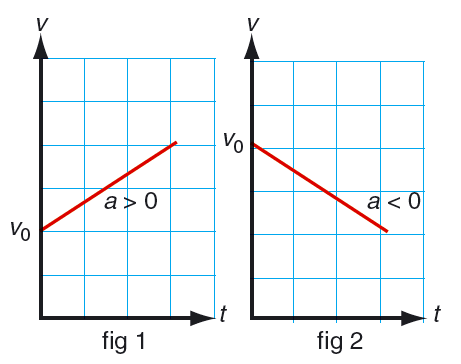
I figur 1 ökar hastigheten jämnt, accelerationen är positiv.
I figur 2 minskar hastigheten jämnt, accelerationen är negativ.
När Ebba är ute och cyklar har hon hastigheten \(11 \text{ m/s}\) vid en bestämd tidpunkt. I en riktigt härlig nedförsbacke lutar hon sig framåt så att accelerationen blir \(0{,}8 \text{ m/s\(^2\)}\). Vilken hastighet har hon efter \( 5{,}0 \text{ s}\)?
Lösning: Vi sätter in värdena i hastighetsformeln och får \[ v = v_0 + at = 11 \text{ m/s} + (0{,}8 \cdot 5{,}0) \text{ m/s} = 15 \text{ m/s} \]
Hur skulle vi kunna räkna ut hur långt Ebba har hunnit efter \( 5{,}0 \text{ s}\)? Som du har sett tidigare i figur 3.15 är hastighetskurvan en rät linje. Då blir medelhastigheten under tiden \( t \) lika med medelvärdet av starthastigheten och sluthastigheten, \[ \bar{v} = \frac{\text{starthastighet} + \text{sluthastighet}}{2} = \frac{v_0 + v}{2} = \frac{1}{2}(v_0 + v) \]
Nu kan vi beräkna den sträcka \(s\) som avverkats under tiden \(t\). Vi får \[s = \bar{v} t = \frac{1}{2}(v_0 + v) t \] Detta är den första sträckformeln vid konstant acceleration.
När ett föremål har konstant acceleration, beräknas sträckan \(s\) under tiden \(t\) som \[ \text{sträckan} = \text{medelhastigheten} \cdot \text{tiden} \text{ eller } s = \bar{v}t \text{ där } \bar{v} = \frac{1}{2}(v_0 + v) \]
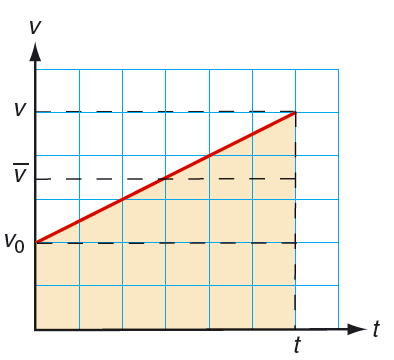
Arean under en \(v\)-\(t\)-graf kan alltid tolkas som den tillryggalagda sträckan. Det betyder att sträckan \(s\) motsvarar arean av det färglagda trapetset i figur 3.16.
Sträckformel 1 innehåller starthastigheten, sluthastigheten och tiden, men inte accelerationen. Det är ofta värdefullt att ha en sträckformel som innehåller accelerationen. Vi sätter in hastighetsformeln \( v = v_0 + at \) i sträckformel 1. \[ s = \frac{1}{2}(v_0 + v)t = \frac{1}{2}(v_0 + \overbrace{v_0 + at}^{v})t = v_0t + \frac{1}{2}at^2 \] Detta är den andra sträckformeln vid konstant acceleration.
När ett föremål har konstant acceleration, beräknas sträckan \(s\) vid tiden \(t\) som \[ s = v_0t + \frac{1}{2} at^2 \]
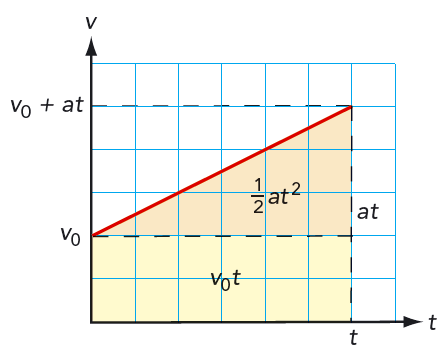
Sträckformel 2 kan du själv komma fram till genom att summera arean av rektangeln och triangeln i figur 3.17.
Ett flygplan startar med den konstanta accelerationen \(3{,}0 \text{ m/s\(^2\)}\). Planet lyfter när hastigheten är \(60\) m/s. Hur lång startbana behöver planet?
Lösning:
Eftersom vi inte känner tiden \(t\) måste vi först beräkna den.
Hastighetsformeln \(v = at\) ger \[ t = \frac{v}{a} = \frac{60}{3{,}0} \text{ s} = 20 \text{ s} \]
Vi sätter in denna tid i sträckformel 2 och får sträckan, \[ s = v_0 + \frac{1}{2}at^2 = 0 + \frac{1}{2} \cdot 3{,}0 \cdot 20^2 \text{ m} = 600 \text{ m} \]
Planet behöver alltså en startbana som är minst \( 600 \) meter lång.
Vi kunde också ha använt oss av medelhastigheten \[ \bar{v} = \frac{0 + 60}{2} \text{ m/s} = 30 \text{ m/s} \] På \( 20 \text{ s}\) hinner planet sträckan \( s = \bar{v} \cdot t = 30 \cdot 20 \text{ m} = 600 \text{ m} \).


