3 Rörelse: 3.5 Fritt fall
 3.5 Fritt fall
3.5 Fritt fall
3.5 Fritt fall
Håll en bomullstuss och en stålkula lika högt ovanför golvet och släpp dem samtidigt. Du ser då att bomullstussen faller långsammare än stålkulan. Tryck ihop bomullstussen och gör om försöket. Nu faller bomullstussen snabbare än i första försöket, men fortfarande långsammare än stålkulan. Vad är det som har förändrats? Bomullstussen är ju lika tung i båda försöken.
Svaret är luftmotståndet. Ju mindre area föremålet vänder mot hastighetsriktningen, desto mindre blir luftmotståndet. Om vi gör samma försök i ett långt glasrör som vi pumpat ut luften ur, så kommer bomullstussen och stålkulan att falla lika snabbt. I glasröret råder vakuum, så där är det bara tyngdkraften som verkar på föremålet under fallet. Då säger man att det faller fritt.
Ett föremål faller fritt när det bara påverkas av tyngdkraften.
När det inte finns något luftmotstånd ger tyngdkraften samma acceleration på alla föremål, oavsett vad de är tillverkade av eller vilken form de har. Den förste som föreställde sig ett fall utan luftmotstånd var Galileo Galilei. Den lag han upptäckte kallar vi Galileis lag.
Alla föremål som faller fritt på samma ställe, faller med samma acceleration.
Allt sedan Galileis tid har forskarna testat lagen med allt större noggrannhet. Resultaten tyder på att Galileis lag är en naturlag. Naturlagar gäller överallt och alltid, men helt säkra på det kan vi aldrig bli. Sådan är fysiken. Men varje gång Galileis lag testas på ett nytt sätt och bekräftas blir vi lite säkrare.
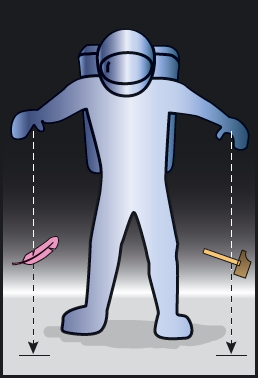
Den amerikanske rymdfararen David Scott gjorde ett skojigt försök på månen, där det inte fi nns någon luft. Han höll en fågelfjäder och en hammare lika högt över marken och släppte dem samtidigt. Se figur 3.19. Fjädern och hammaren föll lika snabbt och nådde marken samtidigt. Försöket visades direkt i TV och bekräftade Galileis lag för miljoner tittare.
Den acceleration som ett föremål får när det faller fritt kallas tyngdaccelerationen. Den har fått symbolen \(g\). Vid havsytan sätter vi \( g = 9{,}82 \text{ m/s\(^2\)} \).
\[ g = 9{,}82 \text{ m/s\(^2\)} \]
| Plats | Breddgrad (°) | Tyngdacceleration (m/s2) |
|---|---|---|
| Quito i Ecuador | \( 0 \) | \(9{,}780\) |
| Hongkong | \(22\) | \(9{,}788\) |
| New York | \(51\) | \(9{,}811\) |
| Stockholm | \(60\) | \(9{,}819\) |
| 2 km över Stockholm | \(60\) | \(9{,}810\) |
| Nordpolen | \(90\) | \(9{,}832\) |
\( 9{,}82 \text{ m/s\(^2\)} \) är ett slags medelvärde som vi använder i exempel och uppgifter. I verkligheten varierar \(g\) bland annat med breddgraden och med höjden över havet.

Titta på bild 3.20 och försök att uppskatta vilken hastighet mannen kommer att ha då gummibandet börjar sträckas. För att kunna göra detta måste du uppskatta avstånden i bilden.
Lösning: Från bilden uppskattar vi att mannen faller en sträcka motsvarande \( 6 \) personlängder, \(6 \cdot 1{,}75 \text{ m} = 10{,}5 \text{ m} \), innan bandet sträcks.
Bortse från luftmotståndet.
Ur sambandet \( \displaystyle s = \frac{1}{2} at^2 \) får vi \( \displaystyle t^2 = \frac{2s}{a} \) \[ t = \sqrt{ \frac{2s}{a} } = \sqrt{ \frac{2 \cdot 10{,}5 }{9{,}82} } = 1{,}5 \text{ s} \] Mannen faller fritt i \(1,5\) s och hastigheten då bandet sträcks blir \[ v = at = 9{,}82 \cdot 1{,}5 \text{ m/s} \approx 15 \text{ m/s}. \]

