4 Newtons lagar: 4.2 Krafter
 Resultantkraft
Resultantkraft
Resultantkraft
Oftast verkar flera krafter samtidigt på ett föremål. Men man kan alltid tänka sig en kraft som har samma verkan som alla dessa krafter har tillsammans. En sådan kraft kallas en resultantkraft.
Resultanten av två eller flera krafter är en tänkt kraft som har samma verkan som de verkliga krafterna har tillsammans.
Newton formulerade tre grundläggande lagar om krafter: Newtons första, andra och tredje lag. Men Newton formulerade en lag till, som den första och andra lagen bygger på. Det är additionslagen för krafter, Newtons nollte lag. Här formulerar vi den för parallella krafter.
Resultanten av två likriktade krafter är lika med summan av krafterna. Resultanten har samma riktning som de två krafterna.
Resultanten av två motriktade krafter är lika med skillnaden mellan den största och den minsta kraften. Resultanten har samma riktning som den största kraften.
En låda påverkas av två parallella krafter \(F_1\) och \(F_2\), där \[ F_1 = 12 \text{ N} \text{ och } F_2 = 4 \text{ N} \]
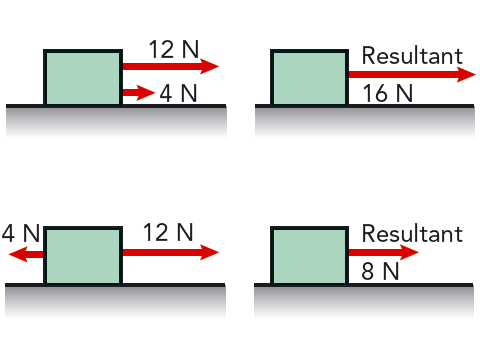
När de två krafterna är likriktade, har de resultanten \[ F_{\text{res}} = F_1 + F_2 = (12 + 4) \text{ N} = 16 \text{ N} \] När de två krafterna är motriktade, har de resultanten \[ F_{\text{res}} = F_1 - F_2 = (12 - 4) \text{ N} = 8 \text{ N} \] Denna resultant har samma riktning som \( F_1 \).
En man och en åsna drar i var sin ände av ett rep. Se figur 4.10. Repet påverkas av två parallella krafter \(F_1\) och \(F_2\), båda på \(12\) N. Hur stor är resultanten?

Lösning: Krafterna verkar i motsatta riktningar. Resultanten av krafterna blir \[ F_{\text{res}} = F_1 - F_2 = (12 − 12) \text{ N} = 0 \text{ N} \]
Verkan av sådana krafter ska vi studera i nästa avsnitt.

