4 Newtons lagar: 4.2 Krafter
 Kraftriktning då krafterna inte är parallella
Kraftriktning då krafterna inte är parallella
Kraftriktning då krafterna inte är parallella
I många fall är inte krafterna parallella men även då måste vi ha en metod att få fram storlek och riktning på de krafter vi är intresserade av. När man adderar två krafter som inte är parallella hamnar resultant kraften någonstans mellan de båda krafterna.
Rebecka och Samara är på ridläger och ska forsla material till lägerplatsen. De får idén att lägga utrustningen i en kanot som de har tillgång till och sedan dra kanoten längs en å som rinner alldeles i närheten av lägerplatsen. De lägger sakerna i kanoten och går sedan på var sin sida om ån och drar kanoten efter sig. Se figur 4.12. Rebecka drar med \(160 \text{ N}\) och Samara drar med \(120 \text{ N}\). Vinkeln mellan de båda krafterna är \(90 \text{ °C}\). Hur stor blir den gemensamma kraften som de drar kanoten med?
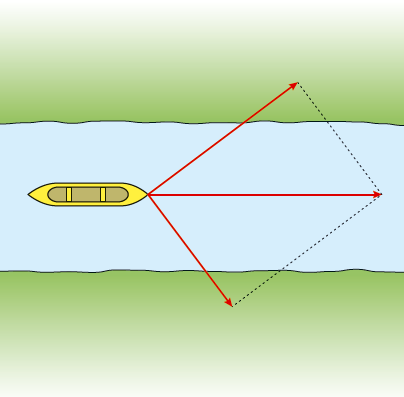
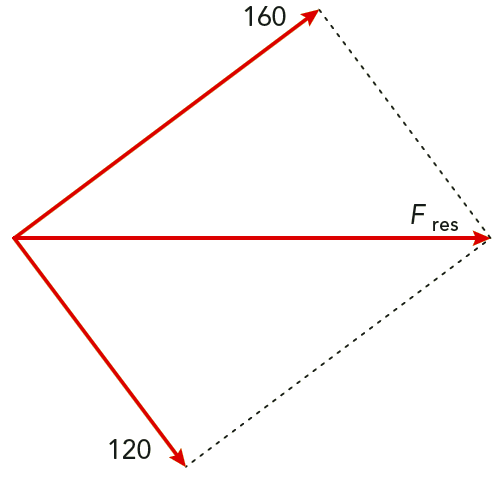
Lösning: Eftersom krafterna är vinkelräta mot varandra kan resultant kraften beräknas med hjälp av Pythagoras sats.
Se figur 4.13
Pythagoras sats ger \[ F^2_{\text{res}} = 120^2 + 160^2 \qquad F_{\text{res}} = 200 \text{ N} \]
Skulle det vara möjligt att göra beräkningarna på andra hållet? Låt oss anta att du visste att resultanten var \(200 \text{ N}\) och att vinkeln mellan resultanten \(F_{\text{res}}\) och den mindre av krafterna, \(F_1\) var \( 53{,}1 \text{°} \). Med hjälp av lite trigonometri kan vi beräkna \(F_1\) och \(F_2\) ur figur 4.14.
\[ F_1 = F_{\text{res}} \cdot \cos 53{,}1 \text{°} \text{ N} = 120 \text{ N} \] \[ F_2 = F_{\text{res}} \cdot \sin 53{,}1 \text{°} \text{ N} = 160 \text{ N} \]
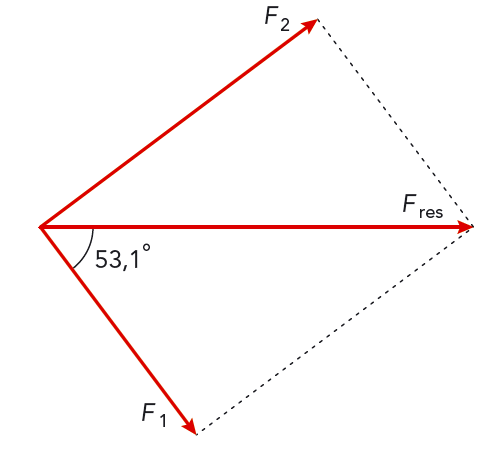
Det här sättet att dela upp en kraft kallas komposantuppdelning.

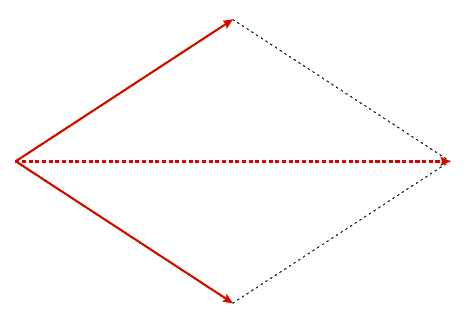
En dag kommer flickornas pappor på besök till ridlägret. Rebecka och Samara är fullt upptagna med att mocka hästarnas boxar och ber därför föräldrarna att gå ut i hagen för att hämta in hästarna. Papporna fäster var sitt grimskaft i hästens grimma och börjar dra. Se figur 4.15. De drar med \(600 \text{ N}\) var men helt utan resultat, hästen rör sig inte ur fläcken. Hur stor är den gemensamma kraften som papporna försöker dra hästen med?
Lösning: Eftersom krafterna inte är vinkelräta mot varandra kan du inte beräkna resultantkraften.
Det enklaste sättet att lösa problemet är att rita av krafterna i en lämplig skala. Var noga med att få samma vinkel som i figuren. Låt varje kraft vara \(3 \text{ cm}\). Nu kan du mäta resultantkraften och ser då att den blir ungefär \(5 \text{ cm}\). Se figur 4.16. Eftersom \(1 \text{ cm}\) motsvarar \(200 \text{ N}\) blir den gemensamma kraften \(1 \ 000 \text{ N}\).
Efter en stund kommer Rebecka ut i hagen och undrar vad papporna håller på med. Hon tar upp en morot ur fickan och vandrar lugnt iväg med sin häst som glatt mumsar på sin morot.

