4 Newtons lagar: 4.3 Newtons första lag
 4.3 Newtons första lag
4.3 Newtons första lag
4.3 Newtons första lag
All erfarenhet visar att när en rörelse upphör, så beror det på att en eller flera krafter motverkar den. Men vad händer om det inte finns några krafter som motverkar rörelsen? Galilei och Newton gjorde det svindlande tankesprånget att föreställa sig att rörelsen då skulle fortsätta i all oändlighet. Den hypotesen har bekräftats så grundligt att den betraktas som en naturlag.
När resultanten av alla krafter som verkar på ett föremål är lika med noll, är föremålet i vila eller i rörelse med konstant hastighet.
Om \( F_{\text{res}} = 0 \), så är hastigheten \(v\) konstant.
Om \(v\) är konstant, så är \( F_{\text{res}} = 0 \).


Newtons första lag uttrycker en insikt om naturen som är mycket viktig, historiskt sett. Lagen jämställer vila och rätlinjig rörelse med konstant hastigheten. Lagen bryter därför mot den uppfattning som rådde före Galilei, nämligen att det behövs en kraft i rörelseriktningen för att hålla ett föremål i rörelse. Galilei och Newton förstod att det inte behövs någon kraft när rörelsen är rätlinjig och hastigheten är konstant. Föremålet fortsätter på grund av en "inre" egenskap, som kallas tröghet. Var klar över att tröghet inte är en kraft!
Newtons första lag säger oss hur ett föremål uppför sig när resultanten av krafterna är noll: Om föremålet är i vila, kommer det att förbli i vila. Om föremålet är i rörelse, kommer det att fortsätta att röra sig med konstant hastighet längs en rät linje. Föremålet kan inte själv förändra sin hastighet. Det är det vi menar med tröghet.
En speciell sorts tåg, som kallas Maglevtåg, kommer upp i en högsta hastighet av drygt \( 430 \text{ km/h}\) . Anledningen till att maglevtågen kan gå så fort är att tågen svävar en bit över marken. Detta sker med hjälp av kraftiga magneter. På så sätt får man nästan helt bort friktionen mellan räls och tåg.

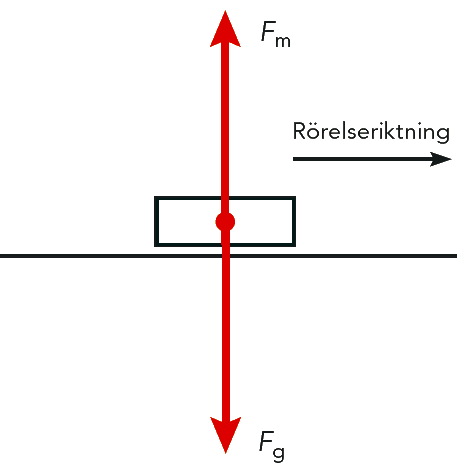
Vid låga hastigheter kan vi bortse från luftmotståndet. Vad kan vi säga om de krafter som verkar på vagnen? Se figur 4.20.
Lösning: Vagnen påverkas av två lodräta krafter. Tyngdkraften \(F_g\) verkar nedåt, och kraften \(F_m\) från magneterna verkar uppåt. Vagnen har inte någon lodrät rörelse. Enligt Newtons första lag måste den resulterande kraften vara lika med noll. Vi får \(F_m + F_g = 0\), det vill säga \( F_m = -F_g \). Det innebär att \(F_g \) och \( F_m \) är lika stora och motriktade. Observera att ingen av de två krafterna verkar i rörelseriktningen.
Leoparden i figur 4.17 befinner sig i jämvikt. Det betyder att leoparden ligger stilla trots att den utsätts både för en gravitationskraft och för en kraft från grenen. De båda krafterna är lika stora och därför är resultantkraften noll. Vår enkla modell fungerar och är mycket användbar i många situationer. Men vi har inte tagit hänsyn till att föremål kan rotera. I figur 4.21 ser du en pinne som ligger stilla. Men om du påverkar pinnen med motriktade krafter i ytterändarna börjar pinnen rotera trots att kraftresultanten är noll.


