4 Newtons lagar: 4.4 Newtons andra lag
 Tyngd
Tyngd
Tyngd
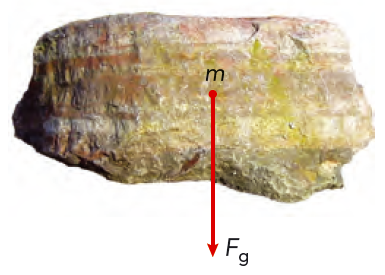
Vi släpper en sten med massan m så att den faller fritt. Se figur 4.24. Stenen påverkas bara av tyngdkraften \(F_g\) och får därför en acceleration lika med tyngdaccelerationen \( g \). Newtons andra lag, \( F_{\text{res}} = ma \), ger oss då \[ F_g = mg \]
\[ \text{Tyngden} = \text{massan} \cdot \text{tyngdaccelerationen} \text{ eller } F_g = mg \]
Tyngden av ett föremål är proportionell mot föremålets massa. Det är en formel som vi får mycket användning för. Formeln gäller oavsett om föremålet är i vila eller i rörelse.
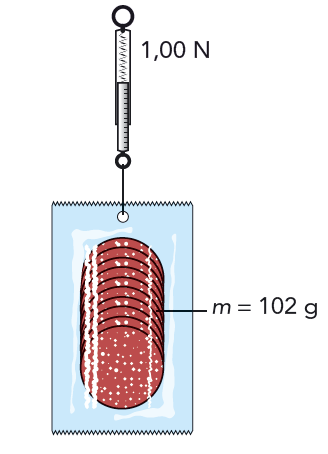
Hur mycket är egentligen en newton – är det en stor eller liten kraft? Tänk dig att du håller en förpackning med rökt korv stilla i handen. Förpackningen har massan \( 102 \) gram. Då känner du en kraft på \( 1 \text{ N}\), eftersom förpackningens tyngd är \[ F_g = mg = 0{,}102 \cdot 9{,}82 \text{ N} = 1{,}00 \text{ N} \]

Vi lyfter en sten lodrätt uppåt. En kort stund har stenen en acceleration på \( 1{,}1 \text{ m/s\(^2\)} \). Massan är \( 7{,}7 \text{ kg}\). Vi ska beräkna hur stor kraft vi lyfter med. Se figur 4.26.
Den resulterande kraften på stenen får vi med hjälp av Newtons andra lag: \[ F_\text{res} = ma = 7{,}7 \cdot 1{,}1 \text{ N} = 8{,}47 \text{ N} \]
Stenen påverkas av två krafter: lyftkraften \(F_l\) uppåt och tyngdkraften \( F_g \) nedåt. Vi får då \[ F_\text{res} = F_l - F_g \] Då blir lyftkraften \[ F_l = F_\text{res} + F_g = (8{,}47 + 7{,}7 \cdot 9{,}82) \text{ N} = 84 \text{ N} \]

