4 Newtons lagar: 4.6 Fysikaliska modeller
 Linjärt samband
Linjärt samband
4.6 Fysikaliska modeller
Linjärt samband
Anders och Elin (AE) ska tillverka en kraftmätare som kan mäta krafter i området \( 0 \text{ N}\) till \( 2,5 \text{ N}\). De har lagt märke till att de flesta kraftmätare på fysiklabbet har en spiralfjäder som sin väsentligaste del. De har också läst att för en spiralfjäder gäller ett linjärt samband mellan dragkraften i ändarna och spiralfjäderns förlängning. Att sambandet är linjärt betyder att om dragkraften är dubbelt så stor blir också förlängningen dubbelt så stor.
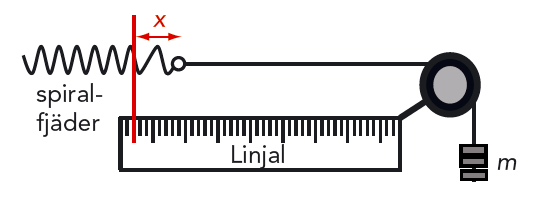
AE hittar en spiralfjäder på fysiklabbet. För att den ska gå att använda som kraftmätare måste de kalibrera den. Att kalibrera den betyder att de ska konstruera en egen kraftskala.
De fäster därför spiralfjäderns ena ände i ett stativ. I andra änden fäster de ett lätt snöre som hänger över en trissa. Se figur 4.30. De hänger sedan olika vikter i snöret och mäter hur mycket spiralfjädern sträcks.
Resultatet av mätningarna skriver de ned i en tabell.
| Massa \(m\) (kg) | Kraft \(mg\) (N) | Förlängning \(x\) (m) |
|---|---|---|
| \(0{,}0 \) | \(0 \) | \(0\) |
| \(0{,}05\) | \(0{,}49\) | \(0{,}025\) |
| \(0{,}1 \) | \(0{,}98\) | \(0{,}052\) |
| \(0{,}15\) | \(1{,}47\) | \(0{,}078\) |
| \(0{,}2 \) | \(1{,}96\) | \(0{,}111\) |
| \(0{,}25\) | \(2{,}45\) | \(0{,}148\) |
| \(0{,}3 \) | \(2{,}94\) | \(0{,}156\) |
För att kunna använda spiralfjädern som kraftmätare måste AE konstruera ett samband som ger dem kraften, \( F \), när de sätter in fjäderns förlängning, \( x \).
Metod 1: De konstruerar ett diagram med passande skala på axlarna så att alla mätpunkter får plats. Sedan ritar de med hjälp av en linjal den räta linje genom origo som ser ut att passa bäst till de uppmätta punkterna. Se figur 4.31.
Den räta linjens funktion är vad de behöver för att avsluta arbetet med sin kraftmätare. Eftersom grafen är rät och utgår från origo har den formen, \[ F(x) = k \cdot x \], där konstanten \( k \) är lutningen \( \displaystyle \frac{\Delta y}{\Delta x} \) på linjen. \(k\), som har enheten \(\text{N/m}\), kommer vi senare att kalla för fjäderkonstant.
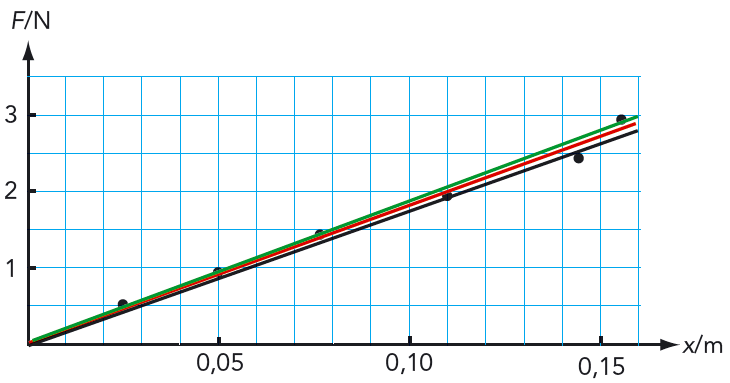
De vickar lite på linjalen för att se vilka olika lutningar som verkar acceptabla. Med hjälp av de olika lutningarna får de en uppfattning om osäkerheten i mätningarna. De kommer fram till att \( k = 18 \pm 1 \text{ N/m} \).
Det betyder att den sökta funktionen är \(F(x) = 18x\), där \(F\) är den kraft som krävs för att töja fjädern med \(x\) meter. När de använder sin fjäder som kraftmätare är det bekvämare att mäta förlängningen i centimeter. Då får de \( F(x) = 0{,}18x \).
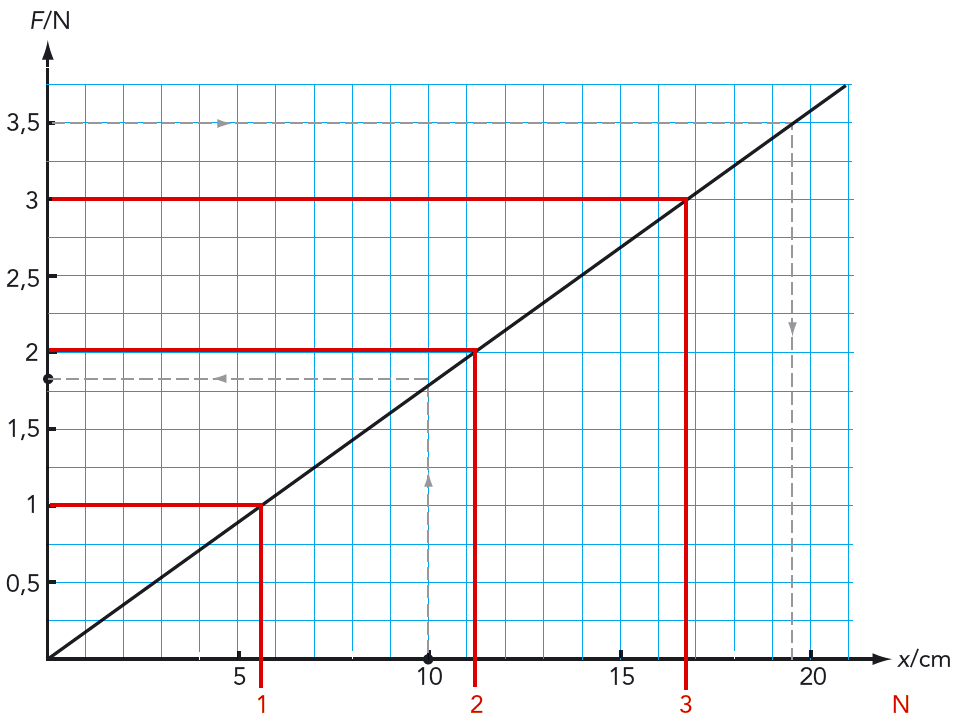
Antingen kan Anders och Elin använda grafen i figur 4.32 för att översätta fjäderns förlängning till kraft. \( 10 \text{ cm}\) förlängning av fjädern kräver en kraft på \( 1{,}8 \text{ N} \). Eller så kan de rita en newtonskala på en linjal, som på #x#-axeln i figuren. En kraft på \( 3{,}5 \text{ N}\) förlänger fjädern med \( 19{,}5 \text{ cm}\). Det betyder att det är \( 19{,}5/3{,}5 = 5{,}6 \text{ cm}\) mellan varje newton på skalan.
Metod 2: Funktionsuttrycket för den räta linjen kan de också få fram genom att använda ett s.k. regressionsprogram på räknaren eller datorn. Då går de in på statistikmenyn och lägger in \(x\)-värdena på list 1 och \(y\)-värdena på list 2. Därefter väljer de linreg. Programmet tar då fram den linje som bäst passar till värdena.
I vårt fall: \[ F(x) = 17{,}5684x + 0{,}0394291 \]
De inser att den funktionen, med alla decimaler, ger sken av en noggrannhet de aldrig kan uppnå i verkligheten. Dessutom ska ju den räta linjen utgå från origo. Deras modifierade funktion blir därför \[ F(x) = 17{,}6x \] Vi ser att metod 1 och 2 ovan ger ungefär samma funktionsuttryck.
Icke-linjärt samband
I räknarens regressionsmeny går det att välja flera andra alternativ än den bästa räta linjen. Väljer du "quadreg" eller \( x^2 \) beroende på typ av räknare, så får du en bit av den parabel (andragradskurva) som passar bäst till mätpunkterna. Med "qubicreg" eller \(x^3\) får du den bästa 3-gradsfunktionen osv.
Anders och Elin fortsätter med att undersöka ett icke-linjärt samband och följande avsnitt visar hur deras laborationsrapport ser ut för dessa försök.

