5 Energi: 5.2 Arbete
 5.2 Arbete
5.2 Arbete
5.2 Arbete

Om du har stor arbetsförmåga skulle man kunna säga att du är energisk. I fysiken använder vi begreppet mekanisk energi på ett liknande sätt. Ett föremål har mekanisk energi när det kan utföra ett arbete. Det måste till ett arbete för att ge ett föremål mekanisk energi. Som du säkert förstår använder vi inte ordet arbete på riktigt samma sätt som du är van vid.
Till vardags kunde det vara ett hederligt arbete att provligga sängar eller läsa böcker. Men detta är inte arbete i fysikalisk mening. Däremot utför du ett arbete när du lyfter något. I fysiken använder vi ordet arbete när krafter verkar på föremål som förfl yttar sig. Se figur 5.1. Men inte ens det är alltid ett arbete. Även om en kraft verkar på ett föremål som fl yttar sig är det inte alltid så att kraften uträttar ett arbete på föremålet. Låt oss först titta på det fall när kraften verkar i rörelseriktningen.

Elsa drar en motsträvig pojke ut på dansgolvet. Se figur 5.2. För att göra det enkelt tänker vi oss att hon drar med en konstant kraft som är parallell med golvet. Om kraften är lika med \(F\) och den motsträvige pojken flyttar sig en sträcka \(s\) i samma riktning som kraften, så utför Elsa ett arbete \(W\) som är lika med kraften multiplicerad med vägen. Vi definierar:
När en kraft verkar på ett föremål som rör sig i kraftriktningen, utför kraften ett arbete på föremålet. Arbetet är lika med kraften multiplicerad med vägen. \[ \text{Arbete} = \text{kraft} \cdot \text{väg} \text{ eller } W = F \cdot s \]
Joule upptäckte bland annat hur elektrisk energi och termisk energi hänger samman med mekanisk energi. Genom att ha en elektrisk strömledare nere i en bestämd mängd vatten, bestämde han energi förlusten i strömkretsen genom att mäta temperaturökningen i vattnet. Detta och en rad andra försök som Joule utförde gav det första experimentella stödet för energiprincipen.
Den här definitionen gäller bara om kraften är konstant och har samma riktning som vägen. Det vill säga nästan aldrig. Det är en väldigt enkel modell som efter hand kommer att leda vidare till mera komplicerade och realistiska situationer.
Eftersom \( \text{Arbete} = \text{kraft} \cdot \text{väg} \) måste enheten för arbete vara \(\text{Nm}\), alltså newtonmeter. Enheten newtonmeter är ekvivalent med enheten joule, \(\text{J}\). Enheten joule är uppkallad efter den engelske fysikern James Joule.
Hur mycket är en joule?
- Det krävs ett arbete på \(1 \text{ J}\) för att lyfta \(1\) liter mjölk \(10 \text{ cm}\).
- Under sommaren träffar i genomsnitt \( 10 \text{ J}\) strålningsenergi från solen varje kvadratdecimeter av Sverige varje sekund.
- \( 4 \ 200 \text{ J}\) kan värma upp \( 1 \) liter vatten \( 1 \) grad.
- Förbränning av \( 1 \) liter bensin ger \( 35 \) miljoner joule.
- Människokroppen behöver ungefär \( 100 \text{ J}\) per sekund för att fungera normalt.
- Varje svensk använder i genomsnitt \( 7 \ 000 \text{ J} \) per sekund.
Jämför den första punkten med de andra. Är det som du hade väntat dig?
Vi lyfter en kasse colaflaskor upp på ett bord. Kassen väger \( 15 \) kg och bordet är \( 80 \) cm högt. Hur stort arbete utför vi på kassen?
Lösning: Enligt Newtons första lag måste vi lyfta med en kraft \( F \) som är lika stor som kassens tyngd. \[ F = mg = 15 \cdot 9{,}82 \text{ N} = 150 \text{ N} \]
Arbetet blir \[ W = F \cdot s = 150 \cdot 0,80 \text{ J} = 120 \text{ J} \]
Nu ska vi utvidga definitionen av arbete till situationer där kraft och väg inte har samma riktning. En kraft \( F \) verkar på ett föremål som flyttar sig en sträcka \( s \). Kraften bildar vinkeln \( \varphi \) med vägen. Se figur 5.3. Då definierar vi arbetet \( W \) som \( F \cdot s \cdot \cos \varphi \). I figuren kan du se att kraften i vägens riktning är \( F \cdot \cos \varphi \).
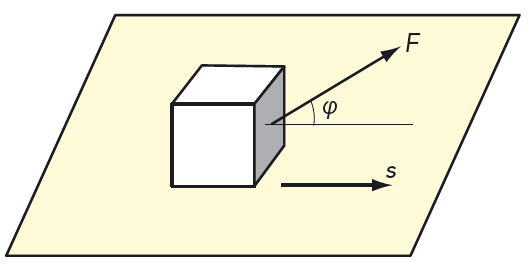
När en konstant kraft verkar på ett föremål som rör sig, utför kraften ett arbete som är lika med kraften multiplicerad med vägen multiplicerad med cosinus för vinkeln mellan kraften och vägen, \[ W = F \cdot s \cdot \cos \varphi \]
Vi måste skilja mellan två fall:
- Kraften utför ett arbete när \( 0 \le \varphi \lt {90 \text{°}} \), för då är \( \cos \varphi > 0 \).
- Kraften utför inte något arbete när \( \varphi = {90} \text{°} \), för då är \( \cos \varphi = 0 \).
En flicka drar en kälke och använder en konstant kraft \( F_1 = 100 \text{ N}\). Vägen är vågrät, och repet bildar vinkeln \(50 \text{°} \) med vägen. Se figur 5.4. Hur stort arbete har hon utfört när kälken har flyttat sig \( 50 \text{ m}\)?
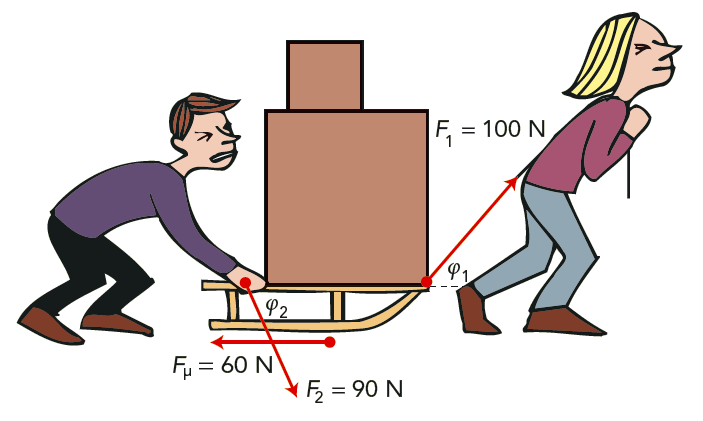
Lösning: Vi kallar arbetet \( W_1 \) och får \[ W_1 = F_1 \cdot s \cdot \cos \varphi_1 = 100 \cdot 50 \cdot \cos 50 \text{°} \text{ J} = 3{,}2 \cdot 10^{3} \text{ J} = 3{,}2 \text{ kJ} \]
Pojken bakom kälken skjuter på med en konstant kraft \( F_2 = 90 \text{ N} \) snett neråt. Vinkeln mellan kraften och vägen är lika med \( 60 \text{°} \). Hur stort arbete utför han på kälken?
Lösning: Vi kallar arbetet \( W_2 \) och får \[ W_2 = F_2 \cdot s \cdot \cos \varphi_2 = 90 \cdot 50 \cdot \cos 60 \text{°} \text{ J} = 2{,}3 \cdot 10^{3} \text{ J} = 2{,}3 \text{ kJ} \]
Som du ser i figuren finns det även en friktionskraft på kälken som är \( F_\mu = 60 \text{ N} \). Friktionen verkar rakt bakåt och utför arbetet \[ W_3 = 60 \cdot 50 \text{ J} = 3{,}0 \text{ kJ} \] Eftersom friktionskraften verkar bakåt motverkas rörelsen.
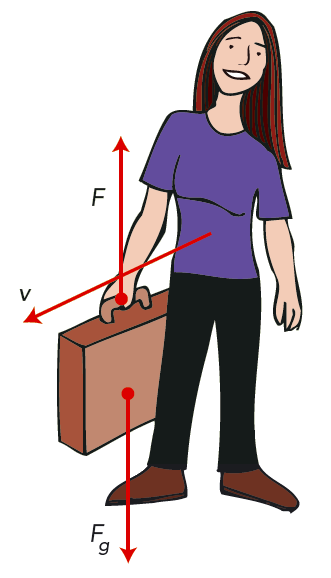
Utöver de tre krafterna vi nämnt hittills, verkar också tyngden \( F_g \) och normalkraften \( F_N \) från underlaget. Men båda dessa krafter verkar vinkelrätt mot vägen och utför därför inget arbete på kälken.
Det finns alltså två fall där vår strävan inte resulterar i något fysiskt arbete. Det ena är när vi använder krafter utan att föremålet flyttar sig. När vägen är lika med noll, är också arbetet lika med noll. Det andra fallet är när kraften verkar vinkelrätt mot vägen. Se figur 5.5.

