5 Energi: 5.4 Potentiell energi
 5.4 Potentiell energi
5.4 Potentiell energi
5.4 Potentiell energi
Kinetisk energi betyder rörelseenergi. Föremål som rör sig kan utföra arbete. Vatten som rör sig kan till exempel driva en turbin. Kan du ge fler exempel på hur rörelseenergi kan överföras genom arbete?

Med potentiell energi är det inte så. Varje typ av potentiell energi är knuten till en bestämd kraft. När vi utför ett arbete på ett föremål mot just den kraften, får föremålet just den typen av potentiell energi. Vi konkretiserar med några exempel. Se figur 5.11.
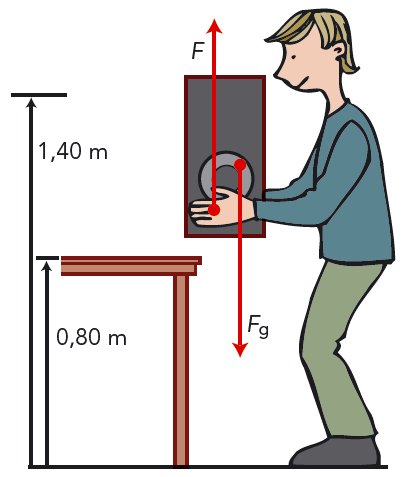
En högtalare med massan \(m\) står på golvet. Du lyfter upp den på ett bord med höjden \(h\). Se figur 5.12. Vi tänker oss att du lyfter lodrätt uppåt med konstant hastighet. Då måste du enligt Newtons första lag lyfta uppåt med en konstant kraft \(F\) som är lika stor som tyngden \(F_g = mg\). Kraften \(F\) utför arbetet\( W = Fh\) på högtalaren. Eftersom \( F = F_g\), kan vi skriva \[W = F_g \cdot h = mgh \] När vi lyfter ett föremål i riktning upp från jordytan, utför vi alltså ett arbete på föremålet, och föremålet får potentiell energi.
Ett föremål med massan m som är på en höjd \(h\) över en fritt vald nollnivå, har en potentiell energi som är \[ W_p = mgh \] där \(g\) är tyngdaccelerationen på platsen.

Lägg märke till att du kan välja nollnivån för den potentiella energin. I tyngdkraftfältet är det ofta naturligt att välja marken eller golvet som nollnivå. Den potentiella energin är alltså given relativt en nollnivå, som du kan välja fritt. Orsaken till att du har den friheten, är att det alltid är differenser i potentiell energi som är viktiga. Om vi faller från en höjd spelar det ingen roll från vilken höjd. Det viktiga är höjdskillnaden! Se figur 5.13.
En högtalare har massan \( m = 9{,}5 \text{ kg} \). Du lyfter först upp högtalaren på ett bord. Se figur 5.12.
Därefter lyfter du högtalaren vidare upp på en hylla \( 1{,}40 \text{ m}\) över golvet. Hur stort arbete måste du då utföra?
Lösning: När du lyfter högtalaren från bordet till hyllan, utför du ett arbete som är lika stort som ökningen av den potentiella energin, \[ W = \Delta W_p = mg \cdot \Delta h = 9{,}5 \cdot 9{,}82 \cdot (1{,}40 - 0{,}80) \text{ J} = 56 \text{ J} \]
Mycket av det som sker i naturen, beror på att föremål rör sig mot lägsta möjliga potentiella energi. Se figur 5.15.