5 Energi: 5.5 Mekanisk energi
 5.5 Mekanisk energi
5.5 Mekanisk energi
5.5 Mekanisk energi
Vi har två grundläggande energiformer i mekaniken: kinetisk energi och potentiell energi. Summan av potentiell energi och kinetisk energi kallar vi mekanisk energi.
I de allra flesta processer bevaras inte den mekaniska energin. Om friktionskrafter finns med i bilden, omvandlas mekanisk energi till termisk energi. Det kan göra mycket ont i handflatorna när du glider nerför ett rep i gymnastiken. I andra fall kan den mekaniska energin bevaras. När ett föremål faller fritt, är det inte utsatt för friktion. Då är det bara tyngden som verkar, och allt det arbete som tyngden utför på föremålet omvandlas till kinetisk energi. Låt oss se på några exempel.
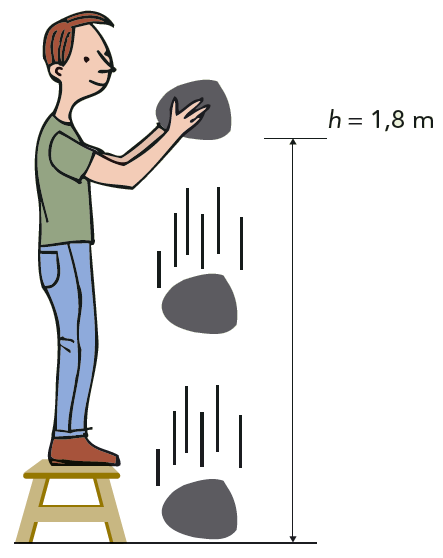
Erik lyfter en \( 7{,}5 \text{ kg} \) tung sten \( 1{,}8 \text{ m} \) upp i luften. Erik släpper stenen. Vilken hastighet har stenen då den slår i marken?
Lösning: Se figur 5.16. När Erik lyfter stenen får den potentiell energi \[ W_\text{p} = mgh = 7{,}5 \cdot 9{,}82 \cdot 1{,}8 \text{ J} = 130 \text{ J} \] När stenen slår i marken har den potentiella energin omvandlats till kinetisk energi.
Vi får då sambandet \( \displaystyle W_\text{k} = \frac{7{,}5v^2}{2} = 130 \text{ J} \) som ger \( v = 5{,}9 \text{ m/s} \).
Vad hade hastigheten blivit om stenen vägt något annat? Låt oss kalla massan \( m \text{ kg} \). Eftersom all potentiell energi övergår i kinetisk energi kan vi skriva \[ \frac{mv^2}{2} = mgh \quad \text{ Här kan vi förkorta med \( m \)! } \] \[ v^2 = 2gh \] \[ v = \sqrt{2gh} \] Som du ser spelar det ingen roll hur mycket stenen väger. I fritt fall har allting samma acceleration.
Kan vi beräkna stenens hastighet då den passerar Eriks knä \( 0{,}8 \text{ m} \) över marken? I förra exemplet beräknade vi att stenens potentiella energi \( 1{,}8 \text{ m} \) över marken var \( 130 \text{ J} \). När stenen är på väg neråt omvandlas den potentiella energin till kinetisk energi. Stenen har både potentiell och kinetisk energi under fallet. Eftersom vi bortser från energiförluster bevaras den mekaniska energin. Vi får då att \[ \frac{mv^2}{2} + mgh = 130 \] Insättning av värden ger \[ \frac{7{,}5v^2}{2} + 7{,}5 \cdot 9{,}82 \cdot 0{,}8 = 130 \] \[ v = 4{,}4 \text{ m/s} \]
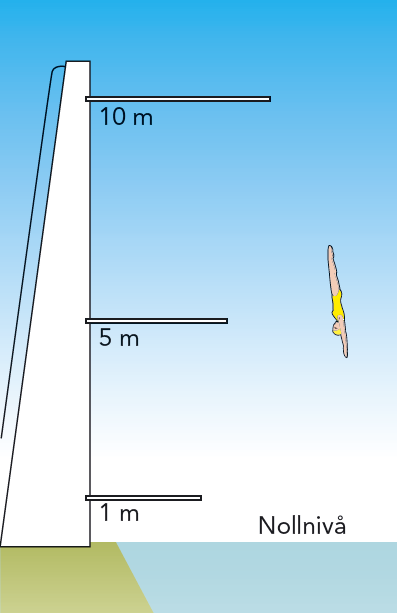
Sodi passerar \(5\)-meterssvikten i hopptornet med hastigheten \(9,9 \text{ m/s}\). Se figur 5.17. Vilken hastighet har hon när hon passerar \(1\)-meterssvikten?
Lösning: Vi kan bortse från luftmotståndet. Då har Sodi konstant mekanisk energi, \( \displaystyle \frac{1}{2}mv^2 + mgh = \frac{1}{2}mv_0^2 + mgh_0 \) , där \(h_0 = 5{,}0 \text{ m}\), \(v_0 = 9{,}9 \text{ m/s}\), \(h = 1{,}0 \text{ m}\) och \(v\) den okända hastigheten. Vi multiplicerar med \(2\) och dividerar med \(m\).
Det ger \[ v^2 + 2gh = v_0^2+2gh_0\text{.} \quad \text{Alltså} \] \[ v = \sqrt{ v_0^2+ 2gh_0 - 2gh } \] \[ v = \sqrt{ 9{,}9^2+ 2\cdot 9{,}82 \cdot 5{,}0 - 2\cdot 9{,}82 \cdot 1{,}0 } \text{ m/s} = 13{,}3 \text{ m/s.} \]
Sodi passerar \( 1 \)-meterssvikten med hastigheten \( 13{,}3 \text{ m/s} \).
Om du tyckte det var svårt att följa uträkningarna kan du sätta in siffrorna direkt i det första sambandet.
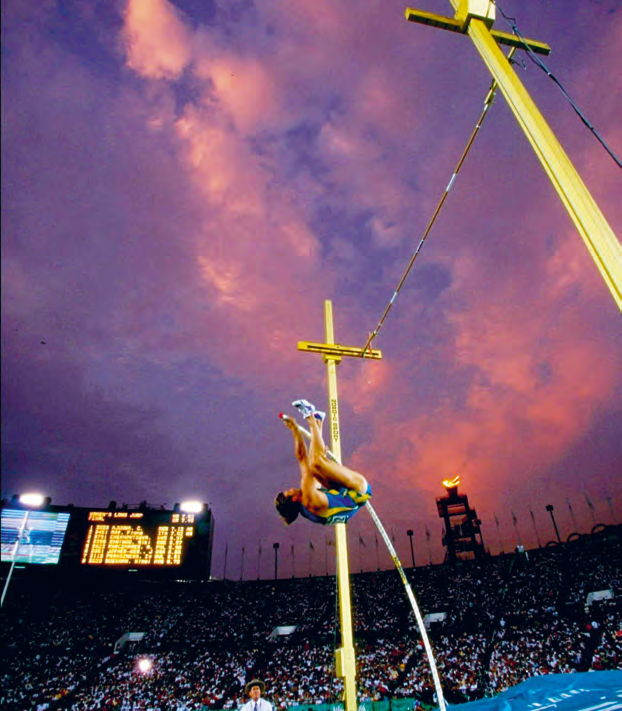
Världens genom tiderna bäste stavhoppare, Sergei Bubka, hade en hastighet på nästan \( 10 \text{ m/s} \) när han sprang mot stavhoppsgropen. Om vi antar att all kinetisk energi kan omvandlas till potentiell energi i hoppet, kan vi beräkna hur högt han kan hoppa. Vi får: \[ mgh = \frac{mv^2}{2} \]
Vi löser ut \( h \) ur sambandet: \[ h = \frac{v^2}{2g} = \frac{10^2}{2 \cdot 9{,}82} \text{ m} = 5 \text{ m} (5{,}09) \]
Med hastigheten \( 9 \text{ m/s} \), som kanske är mer realistisk för en elithoppare, får vi \( h = 4{,}1 \text{ m} \). Före hoppet befinner sig hopparens tyngdpunkt ungefär \( 1 \text{ m} \) över marken. Således kan ribban med detta resonemang ligga i intervallet \( 5 - 6 \text{ m} \). Ännu lite snabbare måste Renaud Lavillenie ha sprungit den 15 februari 2014 då han slog Bubkas inomhusrekord med \( 1 \text{ cm} \). Lavillenie hoppade då \( 6{,}16 \text{ m} \).

