5 Energi: 5.6 Friktion
 Friktionstal
Friktionstal
Friktionstal
Vi gör samma försök som ovan, men sätter en tyngd på kistan. Med samma konstanta hastighet blir både \( F \) och \( F_\mu \) större än första gången. Som du förstår är även normalkraften \( F_\text{N} \) på kistan från underlaget större, eftersom den är lika stor som tyngden av både kistan och vikten. Mätningar visar att förhållandet mellan friktionskraften \( F_\mu \) och normalkraften \( F_\text{N} \) är ungefär konstant när ett föremål glider på ett underlag. Detta förhållande kallar vi friktionstalet \( \mu \), \[ \mu = \frac{F_\mu}{F_\text{N}} \]
Friktionstalet är ett rent talvärde; det saknar enhet. Friktionskraften kan vi nu skriva som \[ F_\mu = \mu F_\text{N} \] Detta betyder att friktionskraften är proportionell mot normalkraften.
Det här är inte en lag utan en regel som gäller i väldigt många praktiska situationer.
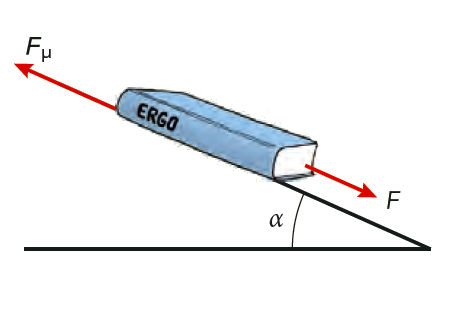
Lägg fysikboken på ett lutande plan så att du kan variera lutningsvinkeln. Se figur 5.22. Om lutningsvinkeln ökas börjar boken vid en viss vinkel att glida neråt. Bestäm friktionstalet om boken väger \( 400 \text{ g} \) och börjar glida vid en lutning på \( 24 \) grader.
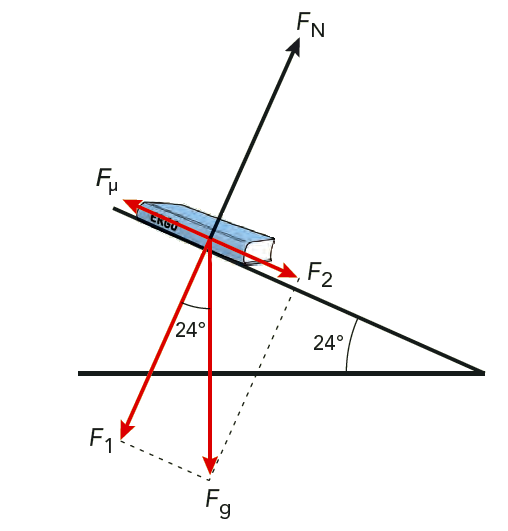
Lösning:
Dela först upp tyngdkraften i komposanter.
Ur figuren får vi \[ F_1 = mg \cos \alpha = 0{,}4 \cdot 9{,}82 \cdot \cos 24 \text{°} \text{ N} = 3{,}6 \text{ N} \] \[ F_2 = mg \sin \alpha = 0{,}4 \cdot 9{,}82 \cdot \sin 24 \text{°} \text{ N} = 1{,}6 \text{ N} \]
Eftersom \[ F_1 \text{ är lika stor som normalkraften } F_\text{N} \text{ på boken och } \] \[ F_2 \text{ är lika stor som friktionskraften } F_\mu \text{ mellan boken och underlaget } \] kan vi skriva \[ \mu = \frac{F_\mu}{F_\text{N}} = \frac{mg \sin \alpha}{mg \cos \alpha} = \tan \alpha = 0{,}45 \]
Eftersom massan kan förkortas bort i ekvationen ovan kommer boken att börja glida vid ungefär samma vinkel även om vi ökar bokens massa. Testa det själv genom att till exempel lägga på några vikter!
Låt oss nu gå lite djupare och se vad som verkligen händer. Gör gärna försöket själv med några olika föremål mot olika underlag. Du kan till exempel prova med ett suddgummi som får glida på en linjal. Du kommer nog att lägga märke till flera saker. Dels att när suddgummit väl kommer på glid så ökar farten. Det accelererar. Dels att det är nästan omöjligt att få det att glida med konstant fart vid samma lutning. Det kommer att glida ryckvis.
Friktionstalet är visst inte helt konstant och \( F_\mu = \mu F_N \) är tydligen inte en helt vattentät regel. Orsaken kan vara att materialet är olika hårt på olika ställen. Det fi nns säkert smuts, oxider eller andra främmande ämnen som bestämmer hur friktionen är på ett visst ställe. Vid mikroskopi i biologin har du säkert någon gång ”limmat” fast ett täckglas med hjälp av en vattendroppe eller en droppe blod. Sedan kan du hålla objektglaset upp och ned utan att täckglaset faller av. Vad kan man då säga om friktionstalet mellan täckglas och objektglas?
Har du sett en Geckoödla någon gång? Om man är uppmärksam kan man ibland se dem på Sydeuropas vitkalkade husväggar, speciellt på kvällen nära en lampa. Där fångar de insekter som dras till ljuset. Man har länge förundrats över att ödlorna tycks kunna röra sig som flugor på väggen. De kan till och med kila omkring på undersidan av taket! De behöver inte ens de små skrovligheterna i väggen. Nej, Geckoödlor kan röra sig lika snabbt på en vertikal eller till och med uppochnedvänd glasyta!

Har de sugkoppar, eller något slags lim? För några år sedan löstes geckomysteriet av några amerikanska forskare som studerade deras fötter med hjälp av elektronmikroskop. Det visade sig att fötterna är täckta av miljontals tunna hårstrån, så kallade seta. Varje seta är lika långt som ett människohår är brett, men slutar i en borste av \( 1 \ 000 \) nya ännu tunnare hårstrån. Toppen av dessa yttersta hårstrån kommer tillräckligt nära molekylerna i det materialet Geckon befinner sig på för att molekylkrafterna mellan spetsen på de tunnaste hårstråna och underlaget ska bli stora. \( 1 \ 000 \) av de tunnaste stråna kan bära vikten av en myra. Alla seta skulle tillsammans kunna bära en vikt på \( 120 \text{ kg} \). Ändå är hårspetsarnas samlade yta mindre än ytan av en enkrona!
Tänk vilket lim vi skulle kunna tillverka om vi kunde kopiera Geckons konststycke! Vilka klätterhandskar! Vi skulle kunna hänga på undersidan av ett glastak i en fingertopp!
Sodi passerar \( 1 \)-meterssvikten med hastigheten \( 13{,}3 \text{ m/s} \).
Till sist kan man undra hur Geckon överhuvudtaget kan lyfta benen från underlaget, eller hur den kan undgå att bli smutsig på fötterna? Kanske kan du fi nna svaret själv genom att söka på webben? Sökord skulle kunna vara Gecko adhesive.

