5 Energi: 5.6 Friktion
 Friktionsarbete
Friktionsarbete
Friktionsarbete
När något glider, verkar friktionen alltid mot rörelsen. Friktionskraften \( F_\mu \) utför ett arbete, som vi kallar friktionsarbetet \(W\). Friktionsarbetet \(W\) längs en vägsträcka \(s\) blir \[ W = F_\mu s \] Friktionsarbetet verkar bromsande. Det betyder att den mekaniska energin minskar.

Efter en olycka på en motorväg i England uppmättes bromsspåren efter en Jaguar till \( 290 \text{ m} \). Polisen mätte att friktionskoefficienten var lika med \( 0{,}80 \) för glidfriktion mellan hjulen och vägen. Vilken hastighet hade Jaguaren strax innan den började tvärbromsa?
Lösning: Om underlaget är horisontellt, är normalkraften lika stor som tyngden. Då kan vi skriva friktionskraften som \( F_\mu = \mu mg \), där \( \mu = 0{,}80 \). Friktionen gör att bilen förlorar all sin mekaniska energi, som blir friktionsarbete.
Nu kan vi beräkna utgångshastigheten \(v_0\). \[ \frac{1}{2}mv_0^2 = F_\mu s = \mu mgs \]
som ger \[ \begin{align*} v_0 = \sqrt{2 \mu gs} &= \sqrt{2 \cdot 0{,}80 \cdot 9{,}82 \cdot 290 } \text{ m/s } \\ &= 67{,}5 \text{ m/s} \\ &\approx 240 \text{ km/h} \end{align*} \]
Är det rimligt att tro att friktionstalet är konstant genom hela bromssträckan? Hur påverkas svaret om det inte är det?
Friktionstalet mellan bilhjulen och vägen beror på hur bra däcken är, och vägens tillstånd. Med bra däck på torr asfalt är friktionstalet för glidfriktion cirka \( 0{,}80 \). Med våt asfalt eller dåliga däck blir friktionstalet mycket lägre. På hal vinterväg kan friktionstalet bli så lågt som \( 0{,}15 \). Formeln i exempel 11 visar att \( \displaystyle \mu mgs = \frac{1}{2} mv_0^2 \ \) på horisontell väg. Det betyder att bromssträckan med låsta hjul blir \[ s = \frac{v_0^2}{2 \mu g} \]
Om friktionstalet halveras, så fördubblas bromssträckan. Om hastigheten fördubblas, så blir bromssträckan fyra gånger så lång! Bilens massa har ingen inverkan.
Ferat sätter fart på sin skateboard och rullar uppför en backe. När skateboarden rullar uppför saktar den ned, stannar och börjar sedan accelerera nedför backen igen. När är accelerationen störst? I uppförsbacken eller i nedförsbacken?
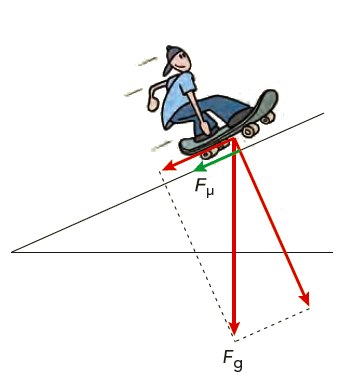

Lösning: För att tydligt se vilka krafter som påverkar accelerationen delar vi upp tyngdkraften i komposanter. Se figur 5.27. När Ferat rullar uppför backen bromsas rörelsen både av tyngdkraftens komposant längs backen och av rullmotståndet. Båda dessa krafter verkar nedför backen. När Ferat rullar nedför backen verkar tyngdkraftens komposant åt samma håll som innan, men rullmotståndet verkar nu uppför backen. Den resulterande kraften och därmed också accelerationen blir därför mindre då Ferat åker nedför backen.

