6 Rörelsemängd: 6.3 Bevarande av rörelsemängden
 6.3 Bevarande av rörelsemängden
6.3 Bevarande av rörelsemängden
6.3 Bevarande av rörelsemängden
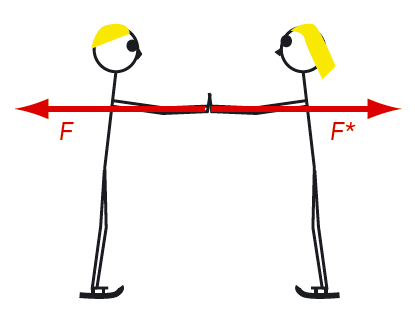
Elin och Per vill undersöka begreppet rörelsemängd. De snörar på sig skridskor och ställer sig mitt emot varandra. Se figur 6.5. Elin knuffar Per med en kraft \(F\) åt vänster. Därmed knuffas Elin med en lika stor motkraft \(F^*\) åt höger, \( F^* = F \). Detta är ett exempel på Newtons tredje lag som vi läste om i kapitel 4.
Elin och Per filmar hela förloppet med en mobilkamera och kan efter några mätningar få fram hastigheterna \(v_\text{Per} = - 0{,}2 \text{ m/s}\) och\( v_\text{Elin} = 0{,}3 \text{ m/s}\). Se figur 6.6.
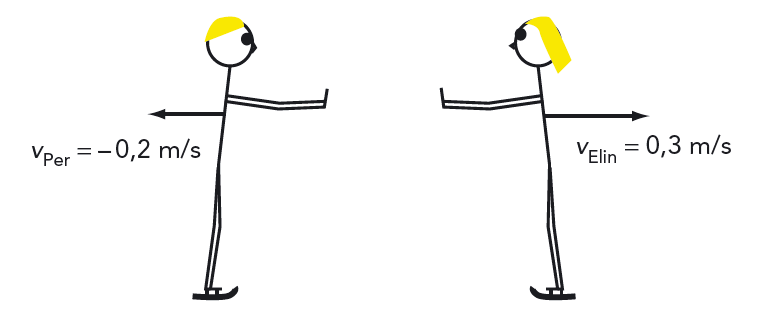
De vill nu jämföra sina rörelsemängder. De vet att Per väger \(75 \text{ kg}\) och att Elin väger \(50 \text{ kg}\).
\[p_\text{Per} = m_\text{Per} \cdot v_\text{Per} = 75 \cdot (-0{,}2) \text{ kgm/s} = -15 \text{ kgm/s} \] \[p_\text{Elin} = m_\text{Elin} \cdot v_\text{Elin} = 50 \cdot 0{,}3 \text{ kgm/s} = 15 \text{ kgm/s} \]
Rörelsemängderna är lika stora men riktade åt olika håll. Observera att deras sammanlagda rörelsemängd är noll både före och efter knuffen. \[ \begin{split} &p_{\text{före}} = p_{\text{efter}} = 0 \\ &p_{\text{före}} = 0 &\text{ (eftersom Per och Elin står stilla) } \\ &p_{\text{efter}}= 0 &\text{ (eftersom \(−15 + 15 = 0 \)) } \end{split} \]
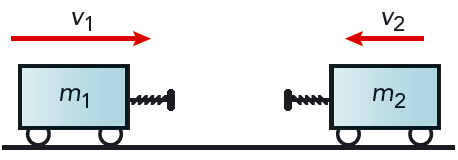
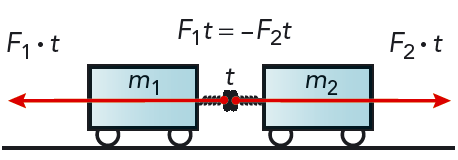
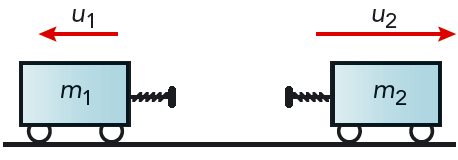
Vi tar ett exempel till. Tänk dig att två vagnar med massorna \(m_1\) och \(m_2\) rör sig utan friktion eller luftmotstånd på en vågrät bana. Hastighetsvektorerna är \(v_1\) och \(v_2\). Se figur 6.7. Vagnarna kolliderar och påverkar varandra med krafter. Kraften \(F_1\) verkar på vagn 1, och kraften \(F_2\) verkar på vagn 2. Krafterna kommer säkert att variera under stöten, men vi tänker oss att krafterna är konstanta, eller att \(F_1\) och \(F_2\) är medelkrafter. Resultatet blir detsamma. Newtons tredje lag medför att de två krafterna är lika stora och motsatt riktade, \[ F_2 = -F_1 \]
Krafterna verkar under lika lång tid, det vill säga under den tid \(\Delta t\) som kollisionen varar. Därför är också impulserna på de två vagnarna lika stora och motsatt riktade, \[ F_2 \Delta t = - F_1 \Delta t\]
Efter att krafterna har verkat under tiden \(\Delta t\), har vagnarna hastigheterna \(u_1\) och \(u_2\). Impulslagen ger \[ F_1 \Delta t = m_1 u_1 - m_1 v_1 \quad \text{för vagn 1} \] \[ F_2 \Delta t = m_2 u_2 - m_2 v_2 \quad \text{för vagn 2} \]
Vi sätter in högerleden av dessa formler i formeln \(F_2 \Delta t = - F_1 \Delta t\). Det ger \[ m_2 u_2 - m_2 v_2 = -(m_1 u_1 - m_1 v_1) \]
Vi ordnar formeln och får \[ m_1 u_1 + m_2 u_2 = m_1 v_1 + m_2 v_2 \]
Denna formel säger oss att den totala rörelsemängden efter kollisionen är lika med den totala rörelsemängden före kollisionen: \[ p_\text{före} = p_\text{efter} \] Med detta har vi kommit fram till en av mekanikens mest grundläggande lagar:
När två föremål kolliderar är den totala rörelsemängden efter kollisionen lika med den totala rörelsemängden före kollisionen, \[ m_1u_1 + m_2u_2 = m_1v_1 + m_2v_2 \]
Här är \(m_1\) massan av föremål 1, \(m_2\) massan av föremål 2, \(v_1\) och \(v_2\) hastigheterna före kollisionen, och \(u_1\) och \(u_2\) hastigheterna efter. Bevarandelagen är generell. Den gäller för alla slags kollisioner mellan två föremål, oavsett vilka krafter som verkar mellan dem.
Två slädar rör sig mot varandra på en vågrät luftkuddebana och kolliderar. Efter kollisionen hänger slädarna ihop. Se figur 6.8. Den ena släden har massan \(m_1 = 0{,}50 \text{ kg}\) och hastigheten \(2{,}0 \text{ m/s}\) före kollisionen. Den andra släden har massan \(m_2 = 0{,}30 \text{ kg}\) och hastigheten \(2,0 \text{ m/s}\) i motsatt riktning. Vad blir den gemensamma hastigheten efter kollisionen om vi kan bortse från friktion?
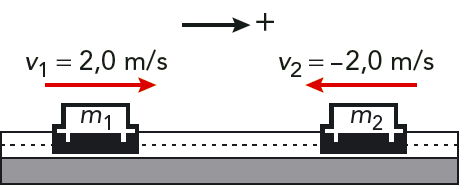
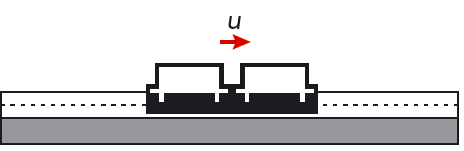
Lösning: Vi väljer positiv riktning längs \(v_1\), det vill säga åt höger i figuren. Då blir \[ v_1 = 2{,}0 \text{ m/s} \quad \text{ och } \quad v_2 = - 2{,}0 \text{ m/s} \] De två slädarna hänger samman efter kollisionen, och vi ska beräkna den gemensamma hastigheten \(u\).
Före kollisionen är den totala rörelsemängden \[ p_{\text{före}} = m_1v_1 + m_2v_2 = ( 0{,}50 \cdot 2{,}0 + 0{,}30 \cdot (- 2{,}0)) \text{ kgm/s} = 0{,}40 \text{ kgm/s} \]
Efter kollisionen är rörelsemängden \[ p_\text{efter} = (m_1 + m_2)u \]
När det inte finns någon friktion, bevaras rörelsemängden. Därför är \(p_\text{efter} = p_\text{före}\) och vi får \[ u = \frac{p_\text{före}}{m_1+m_2} = \frac{0{,}40}{0{,}50 + 0{,}30} \text{ m/s} = 0{,}50 \text{ m/s} \]
Du ser att \(u\) är positiv. Det betyder att de sammanhängande slädarna rör sig åt höger efter kollisionen.

