6 Rörelsemängd: 6.3 Bevarande av rörelsemängden
 Elastisk stöt
Elastisk stöt
Elastisk stöt
Ibland när förlusten av kinetisk energi är relativt liten, väljer vi att bortse från den. Det är bara vissa kollisioner i atomernas mikrovärld som kan vara helt elastiska.
En stöt är elastisk när den kinetiska energin är lika stor efter stöten som före stöten.
Under den korta tid som stöten varar, omformas en del av den kinetiska energin till en form av potentiell energi. Det kan vara elastisk energi, som föremålen får när de trycks samman en aning. Men om stöten är elastisk, så omformas hela den potentiella energin åter till kinetisk energi. Då bevaras systemets kinetiska energi, och vi får energiformeln \[ \frac{1}{2}m_1u_1^2 + \frac{1}{2} m_2u_2^2 = \frac{1}{2} m_1v_1^2 + \frac{1}{2}m_2v_2^2 \]
En pendelkula har massan \(m_1 = 0{,}20 \text{ kg}\). Vi drar ut pendeln åt sidan och släpper den, så att den får hastigheten \(v_1 = 4{,}0 \text{ m/s}\) i nedersta läget. Se figur 6.11. Klossen har massan \(m_2 = 0{,}20 \text{ kg}\). Precis efter stöten får klossen hastigheten \( u_2 = 3{,}0 \text{ m/s} \). Vi ska beräkna pendelkulans hastighet efter stöten och vi ska undersöka om stöten mellan kulan och klossen var elastisk.
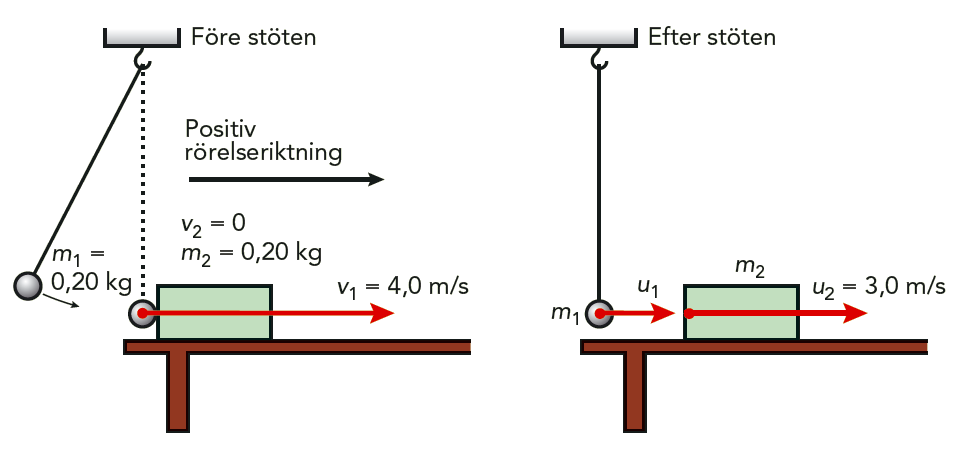
Lösning: Vi väljer positiv riktning åt höger. Efter stöten har kulan hastigheten \(u_1\). Om vi bortser från friktionen i stötögonblicket, bevaras rörelsemängden. Vi får \[ m_1u_1 + m_2 u_2 = m_1 v_1\] som ger \[ u_1 = \frac{m_1v_1 - m_2u_2}{m_1} = \frac{0{,}20 \cdot 4{,}0 - 0{,}20 \cdot 3{,}0}{0{,}20} \text{ m/s} = 1{,}0 \text{ m/s} \]
Du ser att hastigheten \(u_1\) är positiv. Det betyder att kulan rör sig åt höger efter stöten.
Kinetiska energin före stöten var \[ W_\text{k före} = \frac{1}{2} m_1 v_1^2 = \frac{1}{2} \cdot 0{,}20 \cdot 4{,}0^2 \text{ J} = 1{,}6 \text{ J} \]
Kinetiska energin efter stöten är \[ W_\text{k efter} = \frac{1}{2} m_1 u_1^2 + \frac{1}{2}m_2 u_2^2 = \frac{1}{2} \cdot 0{,}20 \cdot (1{,}0^2 + 3{,}0^2) \text{ J} = 1{,}00 \text{ J} \]
Den kinetiska energiförändringen för kula och kloss är \[ \Delta W_\text{k} = W_\text{k efter} − W_\text{k före} = 1{,}00 \text{ J} − 1{,}60 \text{ J} = -0{,}60 \text{ J} \] Stöten var alltså inte elastisk.

