6.4 Ballistisk pendel

Syfte: Målet med försöket var att undersöka om man med hjälp av lagen om rörelsemängdens bevarande indirekt kan mäta farten hos en kastad boll.

Metod: Vi lät en person kasta en boll in i en pappkartong som utgjorde lodet i en pendel. Vi försökte sedan räkna ut bollens hastighet med hjälp av pendelns utslag.

Teori: Metoden bygger på lagen om rörelsemängdens bevarande.

Vi tänker oss att den kastade bollen fastnar i lådan, som är fylld med papperstrassel eller cellplast. Bevarandet av rörelsemängd kräver då att bollens rörelsemängd före kollisionen är precis lika stor som bollens och lådans samlade rörelsemängd omedelbart efter kollisionen, innan mekanisk energi har hunnit avges till omgivningen.

Bollen kommer med farten \( v\) mot lådan.

Bollen fångas upp av lådan.

Lådan med bollen pendlar ut. Tyngdpunkten stiger med \(h\).

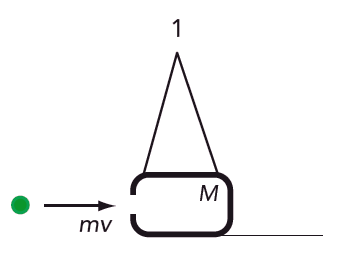
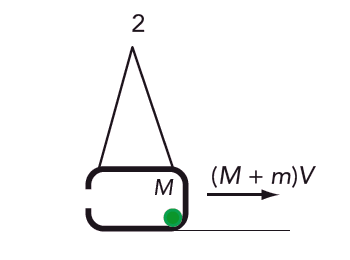
Ekvationer:

Bevarande av rörelsemängd: \(mv = (m + M)V\)

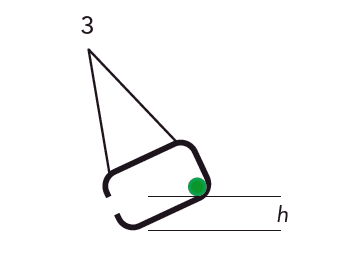
Bevarande av mekanisk energi: \( \displaystyle \frac{(m+M)V^2 }{2} = (m + M)gh \)

Rörelseenergin (omedelbart efter stöten) \(=\) Lägesenergin (när pendeln har maximalt utslag).

Tillsammans utgjorde lådan och snöret en pendel som var \(1{,}0 \text{ m} \) lång. Vi mätte pendelutslaget i horisontell riktning och räknade sedan ut höjden \(h\).

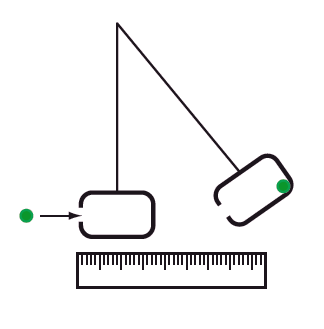
Utförande: Bollen kastades in i lådan och fastnade. Det var lättare att mäta pendelutslaget i horisontell riktning och sedan räkna ut höjden. Till sist hade vi fått fram några resultat som vi betraktade som rimliga.

För att testa metoden och våra resultat gick vi ut och lät vår kastare kasta bollen så långt han kunde. Vi hade läst att med en given fart och utan luftmotstånd går en boll längst när den kastas i \(45\) graders vinkel. Då går den sträckan \(\displaystyle \frac{v^2}{g} \) räknat längs marken.

Resultat:
Bollens massa var \(m = 0{,}063 \text{ kg}\) och lådans massa \(M = 1{,}1 \text{ kg}\). I genom snitt pendlade lådan upp till höjden \(h = 0{,}05 \text{ m}\).

Nu räknade vi bakåt. Bevarande av mekanisk energi från ögonblicket omedelbart efter kollisionen till det största utslaget gav oss \(V\): \[ \frac{(m+M)V^2}{2} = (m+M)gh \implies V = \sqrt{2gh} = 1{,}0 \text{ m/s} \]

Bevarande av rörelsemängd gav oss bollens hastighet före kollisionen: \[ mv = (m+M)V \implies v = \frac{(m+M)V}{m} = 18 \text{ m/s} \]

Till sist jämförde vi den framräknade hastigheten med den hastighet vi kom fram till med hjälp av den maximala kastlängden.

En serie på tre kast gav en genomsnittlig kastlängd på \(44 \text{ m}\). Med hjälp av detta värde kunde vi räkna fram hastigheten: \[ s = \frac{v^2}{g} \implies v = \sqrt{s \cdot g} = 21 \text{ m/s} \]

Slutsats: Vi tycker att vi fi ck en god överensstämmelse (\(18\) resp. \(21 \text{ m/s}\)) mellan de två försöken. Metoden som bygger på rörelsemängdens bevarande var emellertid ganska krävande på grund av svårigheter med en allt mer söndertrasad låda som dessutom insisterade på att rotera. Vi undrar också om vi borde ha haft en lättare låda för att få större noggrannhet? Det procentuella eller relativa mätfelet blir ju stort med små utslag.