7 Termofysik: 7.1 Tryck
 7.1 Tryck
7.1 Tryck
7.1 Tryck
Har du åkt skidor i lös snö någon gång? När du tar av dig skidorna, sjunker du djupt ner i snön. Vad är skillnaden mellan att gå på snön med och utan skidor? Kraften på snön är ju ungefär densamma i båda fallen. Se figur 7.2. Skillnaden ligger i den area som kraften mot snön är spridd över. Ju större area, desto mindre är trycket på snön.

När en kraft \(F\) verkar vinkelrätt mot och jämnt fördelad över en yta med arean \(A\), är trycket \(p\) lika med kraften dividerad med arean, \[ \text{tryck} = \frac{\text{kraft}}{\text{area}} \quad \text{ eller } \quad p = \frac{F}{A} \] Enheten för tryck är pascal, \(\text{Pa}\).
Av definitionen ser du att en pascal är lika med en newton per kvadratmeter, \(1 \text{ Pa} = 1 \text{ N/m\(^2\)}\). Definitionen av tryck gäller också vätskor och gaser.
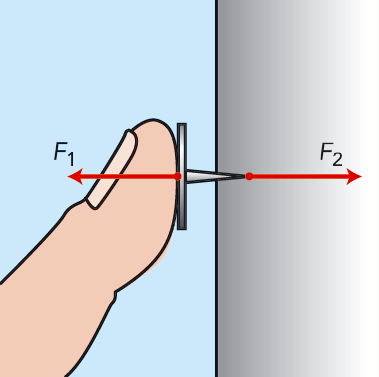
När du trycker in ett häftstift i väggen, verkar det två krafter från häftstiftet: kraften \(F_1\) på fingret och kraften \(F_2\) på väggen. Se figur 7.3. Krafterna är lika stora, men arean \(A_1\) på häftstiftets huvud är mycket större än arean \(A_2\) på spetsen, \(A_1 >> A_2\). Trycket \(p_2\) på väggen från spetsen blir mycket större än trycket \(p_1\) på fingret från huvudet, \(p_2 >> p_1\). Därför går häftstiftet in i väggen och inte in i fingret.
En spikmatta har \(600\) spikar. Avståndet mellan spikarna är \(3 \text{ cm}\). Nu ska vi titta närmare på hur det är att ligga på en sådan spikmatta. Kommer spikarna att tränga in i huden?
För att svara på det gör vi först ett överslag på hur stort trycket mot huden är när en person ligger med ryggen mot spikarna. Vi antar att huden är i kontakt med \(400\) spikar. Lyckligtvis är spikarna inte sylvassa. Kontaktytan mellan en spik och huden är ungefär \(1 \text{ mm\(^2\)}\). Ryggen vilar alltså på en total area \(A = 400 \text{ mm\(^2\)} = 4{,}0 \cdot 10^{-3} \text{ m\(^2\)}\). För en person med tyngden \(F_g = 720 \text{ N}\) blir medelvärdet av trycket från alla spikarna \[ \bar{p}_s = \frac{F_g}{A} = \frac{720}{4{,}0 \cdot 10^{-4}} \text{ Pa} = 1{,}8 \cdot 10^6 \text{ Pa} \] Vad säger det oss? Låt oss göra ett överslag till, så att vi kan jämföra med något vi är mer vana vid.
En person med tyngden \(F_g = 720 \text{ N}\) står på tå på golvet. Arean av tåytorna är ungefär \( A_t = 40 \text{ cm\(^2\)} = 4,0 \cdot 10^{-3} \text{ m\(^2\)} \). Trycket under tåytorna blir \[ \bar{p}_t = \frac{F_g}{A_t} = \frac{720}{4{,}0 \cdot 10^{-3}} \text{ Pa} = 1{,}8 \cdot 10^5 \text{ Pa} \] Överslagen visar att trycket från spikmattan är tio gånger så stort som trycket från golvet när vi står på tå. Men det är ju inte smärtsamt att stå på tå, så vi tål nog trycket från spikmattan också.


