7 Termofysik: 7.2 Temperatur
 Mikroskopisk modell för temperatur
Mikroskopisk modell för temperatur
Mikroskopisk modell för temperatur
Vi vet att naturen är uppbyggd av molekyler. I gaser och vätskor kan molekylerna röra sig fritt om varandra. Men det är förhållandevis ny kunskap. År 1827 gjorde den skotske botanikern Robert Brown (1773–1858) en upptäckt som kunde ha bekräftat molekylhypotesen. Brown lade lite pollen i vatten. Han lade sedan en droppe mellan två glasskivor och tittade på denna i ett mikroskop. Till sin stora förvåning såg han att pollenkornen inte låg stilla, utan vaggade fram och tillbaka. Först 80 år senare insåg man att det var för att pollenkornen bombarderades av vattenmolekyler. Partiklar små som pollenkorn märker att omgivningen inte är kontinuerlig utan består av molekyler i häftig rörelse.
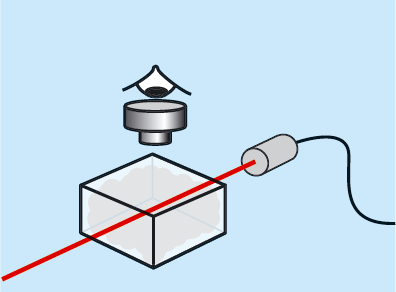
Vi kan göra ett motsvarande försök med en gas som det finns små partiklar i. Se figur 7.16. Vi tänder en veke på så sätt att den ger rök. Sedan placerar vi veken i en glasbehållare och sänder en ljusstråle genom den. När vi tittar på röken i ett mikroskop ser vi att rökpartiklarna rör sig oregelbundet hit och dit. Det tolkar vi som ett resultat av häftiga kollisioner med de pyttesmå molekylerna i luften. Se även figur 7.17.
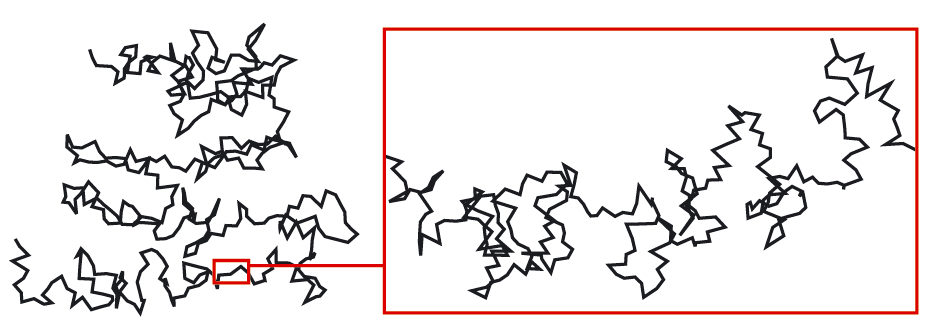
Vår mikroskopiska modell berättar alltså för oss att alla ämnen är uppbyggda av små partiklar som alltid är i rörelse. I en gas rör sig molekylerna i alla riktningar och kolliderar med varandra och med väggarna i gasbehållaren. Vid kollisionerna ändrar molekylerna fart och riktning hela tiden. Vissa har hög hastighet, andra har lägre. Det visar sig att temperaturen i gasen beror på den genomsnittliga kinetiska energin hos gasmolekylerna.
Den absoluta temperaturen \(T\) i en ideal gas bestäms av den genomsnittliga kinetiska energin \(W_k\) hos molekylerna i den gasen, \[ W_{k} = \frac{3}{2} kT \] där \(k = 1{,}38 \cdot 10^{-23} \text{ J/K}\) kallas Boltzmanns konstant.
I formeln \(W_{k} = \frac{3}{2} kT\) står \(W_k\) inte för den kinetiska energin hos en enskild gasmolekyl, utan för medelvärdet av den kinetiska energin för en stor mängd molekyler. Temperaturen i en gas är alltså en kollektiv egenskap hos många molekyler. Det är meningslöst att säga att en enskild molekyl har temperatur.
Om vi sätter våra båda uttryck för kinetisk energi, \(\displaystyle W_{\text{ky}} = \frac{1}{2} mv^2 \) och \(\displaystyle W_k = \frac{3}{2} kT \) lika med varandra, kan vi få fram ett uttryck för medelhastigheten \(\bar v \) för molekylerna i en ideal gas vid olika temperaturer.

Vi får \[ \bar v = \sqrt{\frac{3kT}{m}} \] där \(m\) är molekylmassan. Om två olika gaser har samma temperatur, så är molekylhastigheten störst i den gas som har den lägsta molekylmassan.
En stilla sommardag är temperaturen \(27 \text{ °C}\). Se figur 7.18. Hur stor medelhastighet har molekylerna i luften?
Lösning: Den absoluta temperaturen är \[ T = t + T_0 = (27 + 273) \text{ K} = 300 \text{ K}\] Luften består av ungefär \(78 \ \%\) kvävgas och \(21 \ \%\) syrgas, så vi nöjer oss med att beräkna hastigheten för kvävgas- och syrgasmolekylerna. Molekylmassorna kan vi hitta i tabeller,
\[ m_{\text{N}_2} = 28 \text{ u} = 28 \cdot 1{,}66 \cdot 10^{-27} \text{ kg} = 4{,}6 \cdot 10^{-26} \text{ kg} \] \[ m_{\text{O}_2} = 32 \text{ u} = 32 \cdot 1{,}66 \cdot 10^{-27} \text{ kg} = 5{,}3 \cdot 10^{-26} \text{ kg} \]
Vid temperaturen \(T = 300 \text{ K}\) blir molekylhastigheten för kvävgas \[ \bar{v}_{\text{N}_2} = \sqrt{ \frac{3kT}{m_{\text{N}_2 }} } = \sqrt{ \frac{3 \cdot 1{,}38 \cdot 10^{-23} \cdot 300 }{4{,}6 \cdot 10^{-26}} } \text{ m/s} = 520 \text{ m/s} \]
På samma sätt får vi för syrgas \[ \bar{v}_{\text{O}_2} = 480 \text{ m/s} \] Luftmolekylerna har lika stor genomsnittlig kinetisk energi, men kvävgasmolekylerna har lägre massa och därför högre medelhastighet än syrgasmolekylerna.

