7.3 Tillståndslagen för ideala gaser

Även om vi vet vad som händer på mikronivå, kan vi aldrig observera det direkt. Det vi kan observera är de så kallade makroskopiska storheterna temperatur \(T\), tryck \(p\) och volym \(V\). Eftersom dessa storheter styrs av det som händer på mikronivå finns det ett samband mellan dem även på makronivå. Om vi känner två av dem så kan vi räkna ut den tredje. Eftersom tillståndet för en bestämd mängd gas bestäms av temperaturen, trycket och volymen kommer vi i fortsättningen att kalla dem för gasens tillståndsstorheter. När gasmängden är given, är gasens tillstånd entydigt bestämt av \(p\), \(V\) och \(T\).

Sambandet mellan tillståndsstorheterna ges av tillståndslagen för gaser:

Konstanten beror på vilken gas vi betraktar och hur stor gasmängd vi hanterar. Den blir större för en stor gasmängd än för en liten.

Den ideala gasmodellen utgår från en modell där gasmolekylerna inte tar någon plats och inte påverkar varandra med krafter. I verkligheten däremot är den tillgängliga volymen reducerad med gasmolekylernas samlade volym. Det är ungefär den plats molekylerna skulle ta i sin flytande fas. Trycket reduceras även något av att gasmolekylerna attraherar varandra svagt med molekylkrafter.

I praktiken stämmer tillståndslagen mycket bra för verkliga gaser vid normala värden på tryck och temperatur. Det beror på att medelavståndet mellan molekylerna är så stort att molekylkrafterna för det mesta är mycket små. Den flytande fasens volym är också liten jämfört med gasens volym vid normalt lufttryck och vid temperaturer en bit över smältpunkten. Vatten till exempel tar ungefär 800 gånger större plats som gas än som vätska.

Om den ideala gasen övergår från ett begynnelsetillstånd \( (p_1, V_1, T_1) \) till ett sluttillstånd \( (p_2, V_2, T_2)\), kan vi skriva tillståndslagen som \[ \frac{p_1V_1}{T_1} = \frac{p_2V_2}{T_2} \]

Vi säger att en gas är i normaltillståndet när den har trycket \( p_0 = 101{,}3 \text{ kPa} \) och temperaturen \(T_0 = 273 \text{ K}\). Volymen i normaltillståndet kallar vi \(V_0\). Tillståndslagen för en given gasmängd kan vi då skriva som \[ \frac{pV}{T} = \frac{p_0V_0}{T_0} \] där \( (p, V, T) \) är ett fritt valt tillstånd för gasen.

Fysiktabellen ger densiteten för gasen i normaltillståndet. Om vi kan beräkna den volym en gas skulle ha haft i normaltillståndet, så kan vi också beräkna gasens massa. Massan för en bestämd gasmängd är ju lika stor i alla tillstånd.

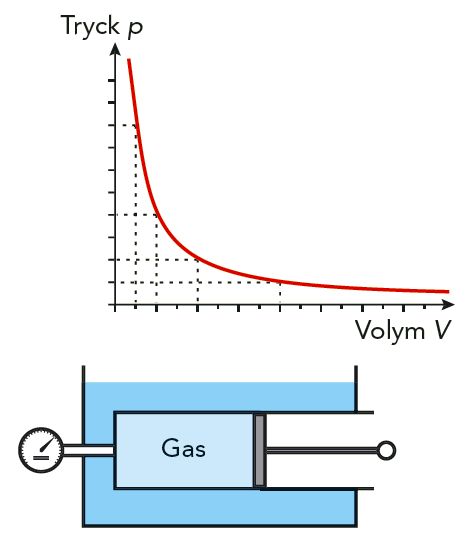
Tillståndslagen är egentligen en kombination av tre gaslagar, som upptäcktes vid en rad olika försök. En av dem är Boyles lag.