7 Termofysik: 7.4 Värme
 Inre energi
Inre energi
Inre energi
Det som förändrade synen på värme, var en rad försök som James Joule gjorde under 1840-talet. Försöken visade att både mekaniskt och elektriskt arbete kan öka temperaturen i ett ämne. Om energin be varas kan det betyda att arbetet omvandlas till en energiform som vi kan kalla inre energi. En ökning av den inre energin leder till att temperaturen stiger, förutom när ett ämne ändrar tillståndsform.
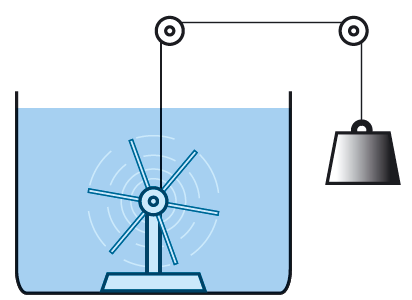
När du ser vatten falla nerför en fors är det inte så svårt att inse att vattnet har energi. Högst upp har vattnet potentiell energi. När vattnet faller, får det högre hastighet och mer kinetisk energi. Men vattnet har också energi oberoende av fallet. Vi vet att vattenmolekylerna är i konstant rörelse. Det betyder att de har en inre kinetisk energi. Men vattenmolekylerna påverkar dessutom varandra med krafter och det finns olika former av bindningsenergier mellan molekylerna. För att dra isär två vattenmolekyler måste vi utföra ett arbete, precis som när vi lyfter en sten i tyngdkraftfältet. Dessa bindnings energier brukar man ibland kalla för inre potentiell energi.
Den inre energin i ett ämne är summan av den inre kinetiska energin och bindningsenergin mellan molekylerna i ämnet.
En ballong med gas har massan \(m\), hastigheten \(v\) och höjden \(h\) över marken. Se figur 7.23. Ballongen har en yttre kinetisk energi \( \displaystyle W_\text{ky} = \frac{1}{2} mv^2 \ \) och en yttre potentiell energi, \(\displaystyle W_\text{py} = mgh\). Ballongen har en yttre mekanisk energi \(W_{\text{mek}}\), som är lika med summan av dessa två, \[ W_\text{mek} = W_{\text{ky}} + W_{\text{py}} \]
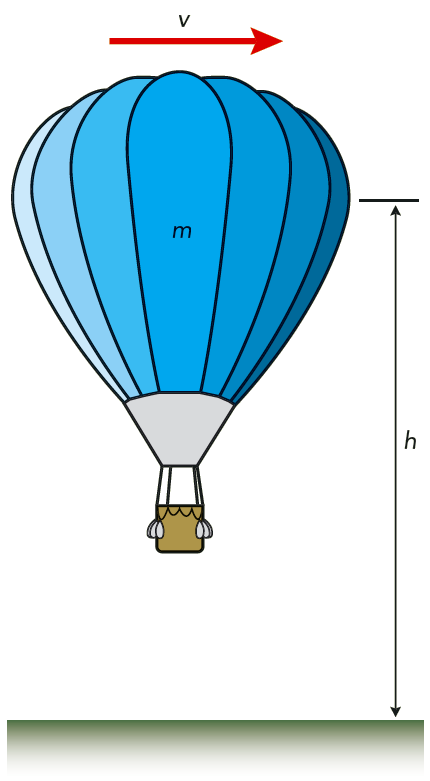
Gasen inne i ballongen i figur 7.23 har även en inre energi. Den består dels av en inre kinetisk energi som är bestämd av gasmolekylernas rörelser, men det finns också bindningsenergier mellan gasmolekylerna. Hur stora dessa bindningsenergier är bestäms av medelavståndet mellan gasmolekylerna.

Vi tänker oss att ballongen i exempel 11 och 12 är fylld med \(100 \text{ kg}\) helium, och att den rör sig med hastigheten \(2{,}0 \text{ m/s}\). Den yttre kinetiska energin är då \[ W_{\text{ky}} = \frac{1}{2} mv^2 = \frac{1}{2} \cdot 100 \cdot 2{,}0^2 \text{ J} = 200 \text{ J} = 0{,}20 \text{ kJ} \]
En heliummolekyl består av en atom med massan \[ m_\text{He} = 4{,}0 \text{ u} = 4{,}0 \cdot 1{,}66 \cdot 10^{-27} \text{ kg} = 6{,}64 \cdot 10^{-27} \text{ kg} \]
Antalet heliummolekyler i gasen är därför \[ N = \frac{m}{m_\text{He} } = \frac{100}{6{,}64 \cdot 10^{-27} } = 1{,}51 \cdot 10^{28} \text{ st} \]
Vid en temperatur på \(20 \text{ °C}\) har dessa heliummolekyler en sammanlagd inre kinetisk energi (termisk energi) på \[ \begin{align*} W_\text{ki} &= N \cdot \frac{3}{2}kT = 1{,}51 \cdot 10^{28} \cdot \frac{3}{2}\cdot 1{,}38 \cdot 10^{-23} \cdot 293 \text{ J} \\ &= 9{,}1 \cdot 10^7 \text{ J} = 91 \text{ MJ} \end{align*} \]
Den inre kinetiska energin är nästan en halv miljon gånger större än den yttre kinetiska energin!
Det är i första hand den inre kinetiska energin som är knuten till temperaturen. Denna energi kallar vi termisk energi. När temperaturen stiger i ett ämne, hänger det ihop med att den termiska energin ökar.
Molekylerna beter sig olika då temperaturen ökar.

I ett fast ämne har molekylerna fasta platser. De hålls fast på sina platser av de elektriska krafterna mellan molekylerna. Men molekylerna vibrerar omkring sina jämviktslägen. Ju kraftigare vibrationerna är, desto större är den termiska energin och desto högre är temperaturen. Om temperaturen ökar ytterligare kommer molekylerna att brytas loss från sina fasta platser. Ämnet börjar smälta.

I en vätska är den termiska rörelsen så våldsam att alla molekylband som bildas omedelbart bryts upp igen. Det gör att molekylerna rör sig friare i förhållande till varandra. Förutom att molekylerna rör sig kan de även rotera. Dessutom kan atomerna i molekylen vibrera kring sina jämviktslägen. Alla dessa rörelser räknas in i den termiska energin.

I en gas kan molekylerna röra sig nästan helt fritt samtidigt som de kan rotera och deras atomer vibrera. Molekylerna i gaser befinner sig vid vanliga förhållanden i genomsnitt på 10 gånger större avstånd till sina grannar än de gör i fasta ämnen och vätskor. Krafterna mellan molekyler avtar mycket snabbt med avståndet. Därför blir krafterna mellan molekyler i gaser vid vanliga förhållanden mycket svaga. Det är förklaringen till att verkliga gaser liknar den ideala gasen vid normala tryck och temperaturer. I en ideal gas finns det ju inga som helst krafter mellan molekylerna så hela den inre energin består av termisk rörelseenergi som är bestämd av temperaturen.

Vid hög temperatur övergår gaser till plasma. Gasmolekylerna kolliderar då så våldsamt med varandra att de spjälkas upp till atomer som mister elektroner och blir joniserade. Eftersom vi här på jorden lever i ganska behagliga temperaturer är plasma ingenting som vi har direkt erfarenhet av; men ute bland stjärnorna är det annorlunda. Ungefär 99 % av all materia i universum består av plasma. Det är lätt att förstå att plasmafysik blir viktig för att förstå vår sol, stjärnorna och universum. Vid mycket hög temperatur, till exempel i stjärnornas inre, blir atomerna fullständigt joniserade. Elektroner och atomkärnor far förbi varandra som fria partiklar.
Vi har talat om låga temperaturer. Eftersom det finns en absolut nollpunkt kunde man kanske undra om det även existerar en absolut topppunkt. Svaret är att det nog inte gör det. Däremot finns det en gräns för hur höga temperaturer som finns i vårt universum just nu. I fysiken talar man faktiskt om universums temperatur. Det är den temperatur som rymden har långt ifrån stjärnorna. Den temperaturen är \(2{,}7 \text{K}\). Det är den temperatur som stenar och stoft får långt ifrån stjärnorna. Det kan innebära att universums lägsta temperaturer någonsin har uppnåtts i laboratorier på en liten planet i Vintergatan!

