7 Termofysik: 7.5 Värmekapacitet
 7.5 Värmekapacitet
7.5 Värmekapacitet
7.5 Värmekapacitet
Om samma mängd vatten och järn mottar lika mycket energi så kommer järnets temperaturökning att vara ungefär 9 gånger större än vattnets.
På fysikspråk säger vi att olika ämnen har olika kapacitet att lagra inre energi. Den förmågan kallas för specifi k värmekapacitet. Specifik värmekapacitet är karaktäristiskt för ett ämne; den är alltså en ämnes konstant. Den specifika värmekapaciteten för vatten är \( 4 \ 200 \text{ J/( kg \(\cdot\) K)} \) och för järn \( 450 \text{ J/(kg \(\cdot\) K)}\).
Våra tidiga släktingar för över en halv miljon år sedan kunde inte själva göra upp eld. Kan du se framför dig hur de höll sig nära varandra under kalla nätter, omgivna av ett hotande mörker? Det var ett mörker som bland annat dolde den sabeltandade tigern som jagade sitt tvåbenta favoritbyte. I en grotta i Kina har arkeologer hittat djupa lager av aska från en 500 000 år gammal eldstad. De tror att eldstaden hölls vid liv under flera generationer av människor som inte själva kunde göra upp eld.
Det som avgör hur mycket energi som behövs för att öka ett föremåls temperatur beror bara på ämnets specifika värmekapacitet om vi utgår från samma mängd och samma temperaturhöjning.

Ett föremål tillförs värme så att temperaturstegringen blir \(\Delta T \). Den energi som går åt är \[ Q = c \cdot m \cdot \Delta T \]
där \(Q\) är den energi som krävs, \(m\) är föremålets massa och \(c\) är den specifika värmekapaciteten för ämnet.
Den specifika värmekapaciteten talar om hur mycket värme vi måste tillföra \(1 \text{ kg}\) av ett ämne för att få en temperaturhöjning på \(1 \text{ °C}\).
Enheten för specifik värmekapacitet är joule per kilogram per kelvin, \(\text{J/ (kg \(\cdot \) K)}\).
Hur mycket energi går det åt för att värma upp \(2{,}0\) liter vatten från \(20 \text{ °C}\) till \(100 \text{ °C}\)?
Lösning: Enligt en tabell är specifika värmekapaciteten för vatten, \(c = 4 \ 190 \text{ J/(kg \(\cdot\) K)}\).
Vattnets massa är \(2{,}0 \text{ kg}\) och \(\Delta T = (100 - 20) \text{ °C} = 80 \text{ °C}\).
Den energi som går åt blir då enligt sambandet \[ Q = c \cdot m \cdot \Delta T = 4 \ 190 \cdot 2{,}0 \cdot 80 \text{ J} = 0{,}67 \text{ MJ} \] Detta motsvarar energin som krävs för att lyfta en bil som väger ett ton nästan \(70 \text{ m}\) upp i luften!
När vi ska koka vattnet i exempel 16 behöver vi ett kärl, och då blir kärlet också varmt. Detta måste vi ta hänsyn till när vi gör våra beräkningar.
I en järngryta med massan \(0{,}700 \text{ kg}\) ska vi koka upp två liter vatten på en kokplatta som avger en effekt på \(1 500 \text{ W}\). Vattnet och grytan har starttemperaturen \(15{,}0 \text{ °C}\). Hur lång tid tar det innan vattnet kokar?
Lösning: Specifika värmekapaciteten för järn \(450 \text{ J/(kg \(\cdot\) K)}\) fås ur tabell.
Vattnet kokar när temperaturen är \(100{,}0 \text{ °C}\), således blir \( \Delta T = (100{,}0 - 15{,}0) \text{ °C} = 85 \text{ °C} \). Värmebehovet blir \[ Q = Q_\text{järn} + Q_\text{vatten} = (450 \cdot 0{,}700 \cdot 85 + 4 \ 190 \cdot 2 \cdot 85) \text{ J} = 7{,}391 \cdot 10^5 \text{ J} \]
Kokplattan avger effekten \(P = 1 \ 500 \text{ W}\). Vi sätter \(P = Q/t\) och får tiden \(t\): \[ t = \frac{Q}{P} = \frac{7{,}391 \cdot 10^5}{1500} \text{ s} = 493 \text{ s} = 8 \text{ min } 13 \text{ s} \]
Gör försöket hemma i köket! (Plattan måste vara varm innan du sätter på grytan.) Då kommer du att upptäcka att uppkokningen tarlängre tid än den du beräknar teoretiskt. Varför?
När man ska mäta specifik värmekapacitet, använder man en värmemätare. I sin enklaste form kan värmemätaren vara ett kärl och en termometer. Kärlet bör vara värmeisolerat. En termosflaska är en bra värmemätare för enkla försök. Men att tala om en termos specifika värmekapacitet blir lite löjligt. Istället undersöker vi bara hur stor energimängd som krävs för att öka termosens temperatur med \(1\) grad och kallar det för termosens värmekapacitet. En bra värmemätare bör ha så låg värmekapacitet som möjligt och dessutom vara värmeisolerande.
Ett föremål tillförs värme så att temperaturstegringen blir \(\Delta T\). Den energi som går åt är \[ Q = C \cdot \Delta T \text{ där \(C\) är värmekapaciteten för föremålet. } \] Enheten för värmekapacitet är joule per kelvin, \(\text{ J/K}\).
En termosflaska med termometer har temperaturen \(20{,}0 \text{ °C}\). Vi fyller termosen med \(0{,}400 \text{ kg}\) vatten som har en temperatur på\( 25{,}0 \text{ °C}\) och sätter på korken. Se figur 7.30. Sluttemperaturen i termosen och vattnet blir \(24{,}8 \text{ °C}\). Vi ska beräkna värmekapaciteten \(C\) för termos flaskan.
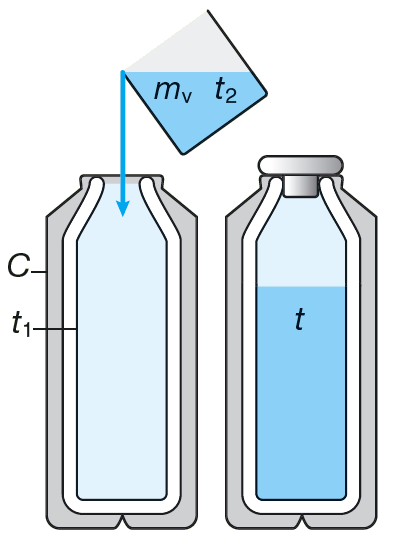
Lösning: Termosen mottar värmen \(\displaystyle Q_1 = C \Delta T_1\).
Vattnet avger värmen \(Q_2 = cm \Delta T_2\), där \(c\) för vatten är \(4 \ 190 \text{ J/(kg \(\cdot\) K)}\). Vi sätter mottagen värme lika med avgiven värme och får ekvationen \[ C \Delta T_1 = cm \Delta T_2 \] Värmekapaciteten \(C\) blir \[ C = \frac{cm \Delta T_2}{\Delta T_1} = \frac{4190 \cdot 0{,}400 \cdot (25{,}0 - 24{,}8) }{(24{,}8 - 20{,}0)} \text{ J/K} = 70 \text{ J/K} \] Detta är en liten värmekapacitet, och det är en viktig egenskap för termosen. När vi fyller varm choklad i en kall termos, vill vi att chokladen ska vara varm efteråt också.

