8 Klimat och väder: 8.3 Olika väderfenomen
 Från sjöbris till monsun
Från sjöbris till monsun
Från sjöbris till monsun
En varm sommardag ligger du och solar på stranden. Efter ett tag känner du dig alldeles för varm och bestämmer dig för att ta ett svalkande dopp i havet. På vägen ned till vattnet bränner du dig nästan under fötterna på den solvarma sanden. Efter det svalkande doppet återvänder du till din filt igen och njuter av sommarsolen.
Marken har alltså värmts upp mer än havet. Luften ovanför stranden blir då varm, utvidgar sig och sväller uppåt. Detta startar cirkulationen, precis som i försöket med vannan, och det börjar blåsa en vind från havet in över land. Vi har fått en sjöbris. Se figur 8.8.
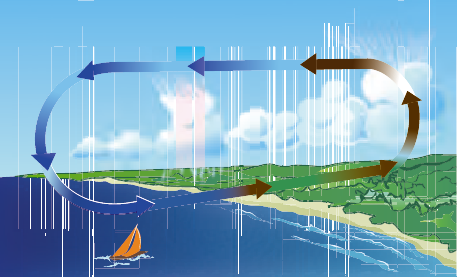
Ibland ersätts sjöbrisen på natten av en landbris som har precis samma drivkrafter. Men nu är det marken som kyls av och blir kallare än vattnet. Då blir effekten den motsatta, en vind från land ut över havet.
Temperaturskillnader ger upphov till tryckskillnader som i sin tur resulterar i att luftmassor rör sig. Ju större temperaturskillnaden är desto kraftigare blir vinden.
Det här var ett exempel på en lugn och fin sommarbris i Sverige. Men samma mekanismer ligger bakom de väldiga monsunvindarna, sommarmonsuner (sjöbris) och vintermonsuner (landbris). Där är det temperaturskillnaderna mellan de varma tropikerna och de kalla polar områdena som är drivkraften.
I förra kapitlet läste du om tillståndslagen för en ideal gas. Då visade vi att tillståndet för en bestämd mängd gas bestäms av temperaturen, \(T\), trycket, \(p\) och volymen \(V\). Det som hände på stranden innan sjöbrisen satte igång är en direkt tillämpning av den ideala gaslagen. Se exempel 3.
En luftmassa med volymen \(1 \text{m^\(3\)}\) har en temperatur på \(17 \text{ °C}\). Beräkna hur stor volymen blir då temperaturen ökar till \(27 \text{ °C}\). Vi antar att trycket är oförändrat.
Lösning: Vi börjar med att skriva upp de värden som vi känner till. \[ V_1 = 1 \text{ m\(^3\)}, \quad T_1 = 17 \text{° C} = 290 \text{ K}, \quad T_2 = 27 \text{ °C} = 300 \text{ K}, \quad p_1 = p_2. \]
Ideala gaslagen ger oss sambandet: \[ \frac{p_1V_1}{T_1} = \frac{p_2V_2}{T_2} \]
Vi löser ut \(V_2\) och får: \[ V_2 = \frac{p_1 V_1 T_2}{p_2 T_1} = \frac{p_1 \cdot 1 \cdot 300}{p_2 \cdot 290} = 1{,}034 \text{ m\(^3\)} \] Volymen har således ökat till \(1,034 \text{ m\(^3\)}\). Skillnaden är \(34\) liter.

