1c 1. Aritmetik och algebra: 1.1 Kvadratrötter och kubikrötter
 Kubikrötter
Kubikrötter
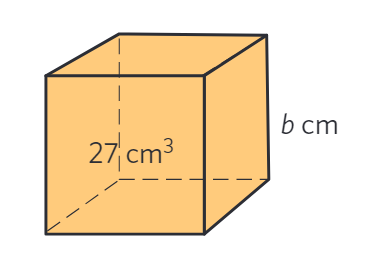
En kub har volymen #27# cm#^3#. Hur lång är dess kant?
Vi låter kanten vara #b# cm. För en kub gäller att #\textit{kantlängd} \cdot \textit{kantlängd} \cdot \textit{kantlängd} = \textit{volym}#, så #b \cdot b \cdot b = 27#.
Den som kan sin multiplikationstabell inser snart att #b = 3#, eftersom #3 \cdot 3 \cdot 3 = 27#.
Kantlängden är alltså #3# cm.
Vi säger att kubikroten ur #27# är #3# och skriver #\sqrt[3]{27} = 3#.
Kubikrot
Kubikroten ur talet #a# betecknas #\sqrt[3]{a}#. Det gäller att #\sqrt[3]{a} \cdot \sqrt[3]{a} \cdot \sqrt[3]{a} = a #
Kubikroten ur talet #a# betecknas #\sqrt[3]{a}#. Det gäller att #\sqrt[3]{a} \cdot \sqrt[3]{a} \cdot \sqrt[3]{a} = a #
En kub har volymen #10# m#^3#. Hur lång är dess kant?
Längden måste var lite större än #2# m, men betydligt mindre än #3# m. (Varför?).
Det exakta svaret är #\sqrt[3] 10#.
Med något digitalt verktyg kan vi bestämma närmevärdet #\sqrt[3] 10 \approx 2,15443#
Längden måste var lite större än #2# m, men betydligt mindre än #3# m. (Varför?).
Det exakta svaret är #\sqrt[3] 10#.
Med något digitalt verktyg kan vi bestämma närmevärdet #\sqrt[3] 10 \approx 2,15443#
Med GeoGebra beräknar du ett närmevärde för #\sqrt[3] 10# så här:
Välj önskat antal decimaler under Inställningar. Välj
Visa-CAS. Klicka på verktyget #\approx#. Skriv i CAS-fönstret: nrot(10, 3). Tryck
ENTER. 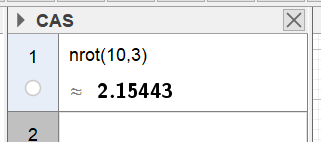
För att få kvadratroten, skriver du #2# i stället för #3#.
Med den matematik vi hittills använt, kan vi inte dra kvadratroten ur negativa tal. När ett tal på tallinjen multipliceras med sig självt, blir produkten alltid noll eller större. Att dra kubikroten ur ett negativt tal går däremot bra.
Eftersom #(-2) \cdot (-2) \cdot (-2) = -8# är #\sqrt[3] {-8} = -2#
Räkneregler för kubikrötter
#\sqrt[3] {a\cdot b} = \sqrt[3] a\cdot \sqrt[3] b#
#\sqrt[3] {a\cdot a \cdot a} = \sqrt[3] a\cdot \sqrt[3] a\cdot \sqrt[3] a = a#
#\sqrt[3] \frac{a}{b} = \frac{\sqrt[3] a}{ \sqrt[3]b}#

