1c 1. Aritmetik och algebra: 1.2 Tal i potensform
 Exponenter som inte är heltal
Exponenter som inte är heltal
För alla tal #a# är #a^1 = a#. Minns också räknereglerna för kvadrat- och kubikrötter:
För ett tal #a# som är noll eller större gäller \[ \sqrt{a} \cdot \sqrt a = a \quad \text{ och } \quad \sqrt[3]{a} \cdot \sqrt[3]{a} \cdot \sqrt[3]{a} = a\]
Detta och räknereglerna för potenser gör det möjligt att skriva rotuttryck i potensform.
För ett tal #a# som är noll eller större gäller \[ \sqrt{a} = a^{\frac{1}{2}} \quad \text{ och } \quad \sqrt[3]{a} = a^{\frac{1}{3}}\]
Räknereglerna för rottal och potenser stämmer överens
\[ \sqrt{a} \cdot \sqrt{a} = a^{\frac{1}{2}} \cdot a^{\frac{1}{2}} = a^{\frac{1}{2} + \frac{1}{2}} = a^{\frac{2}{2}} = a^1 = a \]och
\[ \sqrt[3]{a} \cdot \sqrt[3]{a} \cdot \sqrt[3]{a}= a^{\frac{1}{3}} \cdot a^{\frac{1}{3}} \cdot a^{\frac{1}{3}} \cdot = a^{\frac{1}{3} + \frac{1}{3} + \frac{1}{3}} = a^\frac{3}{3} = a^1 = a \]Även de övriga räknereglerna för potenser fungerar och med hjälp av dem kan vi komma fram till andra exponenter som inte är heltal.
a)
\[ \sqrt[3] 8 = 8^{\frac{1}{3}} = 3 \quad \text{ och } \quad 2\cdot 2=8^{\frac{1}{3}}\cdot 8^{\frac{1}{3}}=8^{\frac{1}{3}+\frac{1}{3}}=8^{\frac{2}{3}}=4 \]
b)
\[9^{\frac{5}{2}}=9^{\frac{1}{2}\cdot 5}=\left(9^{\frac{1}{2}}\right)^5=3^5=243\]
c)
\[ -125^{\frac{1}{3}}=-\left(125^{\frac{1}{3}}\right)=-5 \]
Observera att potensens bas är positiv i c). En exponent “binder starkare” än ett minustecken.
Exponenten i en potens kan vara vilket rationellt tal, bråktal, som helst. Men om exponenten inte är heltal, måste basen i potensen vara noll eller större.
Om #n# och #m# är heltal, är #a^{\frac{1}{n}}# ett tal sådant att #\left(a^{\frac{1}{n}}\right)^n=a# och #a^{\frac{m}{n}}=\left(a^{\frac{1}{n}}\right)^m#
Om #n# och #m# är heltal, är #a^{\frac{1}{n}}# ett tal sådant att #\left(a^{\frac{1}{n}}\right)^n=a# och #a^{\frac{m}{n}}=\left(a^{\frac{1}{n}}\right)^m#
a)
#\left(7^{\frac{1}{4}}\right)^4=7#
b)
#0,001^{\frac{2}{3}}=\left(10^{-3}\right)^{\frac{2}{3}}=\left(10^{-3}\right)^{\frac{1}{3}\cdot 2}=10^{-3\cdot \frac{1}{3}\cdot 2}=10^{-2}=0,01#
c)
#16^{-\frac{1}{4}}=\dfrac{1}{16^{\frac{1}{4}}}=\dfrac{1}{(2\cdot 2\cdot 2\cdot 2)^{\frac{1}{4}}}=\dfrac{1}{2}#
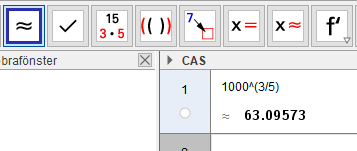
Med GeoGebra beräknar du ett närmevärde för #1000^{\frac{3}{5}}# så här:
Välj önskat antal decimaler under Inställningar. Välj Visa-CAS. Klicka på verktyget #\approx#. Skriv i CAS-fönstret: 1000^(3/5). (Glöm inte parentesen.) Tryck ENTER.