1c 1. Aritmetik och algebra: 1.1 Kvadratrötter och kubikrötter
 Kvadratrötter Del I
Kvadratrötter Del I
 |
En kvadrat har arean #25 # cm#^2#. Hur lång är kvadratens sida? |
För att lösa problemet måste vi hitta ett tal som är sådant, att talet multiplicerat med sig självt får värdet #25#. Om vi kallar talet för #a# får vi problemet #a\cdot a# = #25 # att lösa.
Här är det enkelt att se, med huvudräkning, att lösningen är #a# = #5 # eftersom #5 · 5 = 25. #
Vi säger att "#5 # i kvadrat är #25#". Uttryckssättet hänger ihop med det geometriproblem vi just har löst. Andra exempel på "kvadrattal" är #4#, #9#, #16 # och #36 # eftersom #2 # i kvadrat är #4#, #3 # i kvadrat är #9#, #4 # i kvadrat är #16 # och #6 # i kvadrat är #36#.
En matematisk formulering av lösningen innehåller begreppet kvadratrot.
Kvadratroten ur #25 # är #5#, eftersom #5 · 5 = 25#. Vi skriver detta #\sqrt {25} = 5#.
|
Med kvadratroten ur ett positivt tal #a# menar vi det positiva tal vars kvadrat är #a#. Vi skriver #\sqrt a #. |
Med hjälp av kvadratrot kan vi lösa ett annat, liknande problem.
| En kvadrat har arean #21# cm#^2#. Hur lång är kvadratens sida? |
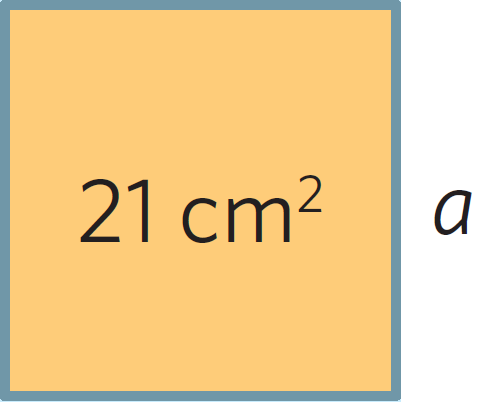 |
Här hittar vi inget heltal som passar. Eftersom #4 · 4 = 16 # och #5 · 5 = 25 # så måste svaret ligga någonstans mellan #4 # och #5. #
Lösningen till problemet är att sidan är #a = \sqrt {21} \approx 4,582575695# (avrundat värde). Det exakta värdet är #a = \sqrt {21} #.
Om sidan är #\sqrt {21} # cm är arean #\sqrt {21}# cm #\cdot# #\sqrt {21}# cm #= 21# cm#^2#.

