Potenser med heltalsexponenter

1c 1. Aritmetik och algebra: 1.2 Tal i potensform

Potenser med heltalsexponenter

Additionen #4 + 4 + 4 + 4 + 4 # kan vi skriva som en produkt: #5 · 4. #

Även en upprepad multiplikation kan skrivas enklare. Produkten #5 · 5 · 5 # skriver vi i stället #5#^#3#.

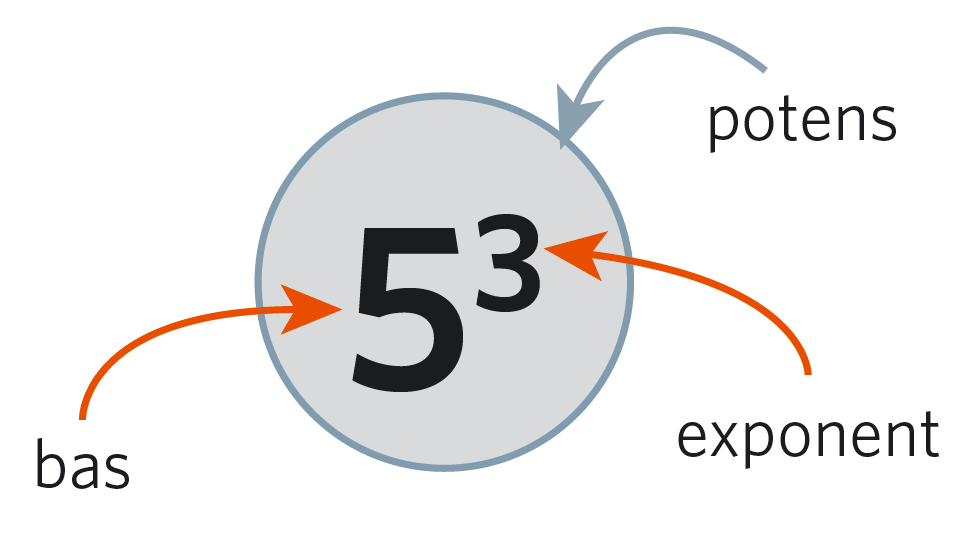
Skrivsättet kallas potensform. #5#^#3# kallas för en potens och utläses
"#5 # upphöjt till #3#". #5 # är bas och #3 # är exponent.

Vi beräknar potenser före multiplikation och division, till exempel #5 · 2#^#3# = #5 · 8. #

Så här gör vi när vi räknar med potenser:

Multiplikation av potenser
#4^5 \cdot 4^2 = 4 \cdot 4 \cdot 4 \cdot 4 \cdot 4 \cdot 4 \cdot 4 = 4^7#	Vi adderar exponenterna.
Division av potenser
#\frac{{{5^4}}}{{{5^2}}} = \frac{{5 \cdot 5 \cdot 5 \cdot 5}}{{5 \cdot 5}} = {5^{4 - }}^2 = {5^2}#	Vi subtraherar exponenterna.
#\frac{{{5^2}}}{{{5^4}}} = \frac{{5 \cdot 5}}{{5 \cdot 5 \cdot 5 \cdot 5}} = \frac{1}{{{5^2}}} = {5^{ - 2}}#	Enligt regeln för division av potenser gäller #\frac{{{5^2}}}{{{5^4}}} = {5^{^{2 - 4}}}={5^{ - 2}}# Slutsatsen blir att #\frac{1}{{{5^2}}} = {5^{ - 2}}#.
#\frac{{{5^2}}}{{{5^2}}} = {5^{^{2 - 2}}} = {5^0} = 1#	#\frac{{{5^2}}}{{{5^2}}} =1# eftersom ett tal dividerat med sig självt blir 1. Slutsaten blir att #{5^0} = 1#
Potens av en potens
#({5^2})^3 = {5^2} \cdot {5^2} \cdot {5^2}=# #= {5^{2 + 2 + 2}} = {5^{2 \cdot 3}} = {5^6}#	Vi multiplicerar exponenterna.
Potens av en produkt
#(5 \cdot 2)^3# = #5 \cdot 2 \cdot 5 \cdot 2 \cdot 5 \cdot 2 =# #=5 \cdot 5 \cdot 5 \cdot 2 \cdot 2 \cdot 2 = 5^3\cdot\,2^3#	Vi upphöjer varje faktor i parentesen.
Potens av en kvot
#{\left( {\frac{2}{3}} \right)^2} = \frac{2}{3} \cdot \frac{2}{3} = \frac{{{2^2}}}{{{3^2}}}#	Vi upphöjer nämnare och täljare var för sig.

#\,#

Räkneregler för potenser

#a^x \cdot a^y = a^{x+y}#	Vid multiplikation av potenser med samma bas adderas exponenterna.
#\frac{{{a^x}}}{{{a^y}}} = {a^{x - y}}#, #(# #a# #\ne# #0) #	Vid division av potenser med samma bas subtraheras exponenterna.
#\frac{1}{{{a^x}}} = {a^{ - x}}#, (#a\ne 0#)	En positiv exponent i nämnaren kan skrivas som en negativ exponent i täljaren.
#a^0=1#, (#a \ne 0#)	Allt som upphöjs till #0 # blir #1#.
#(a^x)^y=a^{xy}#	Vid potens av en potens multipliceras exponenterna.
#(a \cdot b)^x = a^x \cdot b^x#	Vid potens av en produkt upphöjs varje faktor för sig.
#{\left( {\frac{a}{b}} \right)^x} = \frac{{{a^x}}}{{{b^x}}}#, #(b\ne 0)#	Vid potens av en kvot upphöjs nämnare och täljare för sig.

#\,#

Kontroll

Vad kallas #5#:an och vad kallas #3#:an i potensen #5^3#?
Vad blir #3^0#?
Hur gör du med exponenterna vid

a) multiplikation av potenser med samma bas?

b) division av potenser med samma bas?

c) en potens av en potens?

Svar

Basen är #5#, exponenten är #3#.
#3^0=1#
a) Adderar exponenterna.

b) Subtraherar exponenterna.

c) Multiplicerar exponenterna.

#\,#

Skriv som en potens med hjälp av räknereglerna.

#7^2\cdot 7^6#
#\,#

#\,#
Här har vi multiplikation av två potenser med samma bas och vi adderar då exponenterna.

#7^2 \cdot 7^6 =7^{2+6}=7^8#

Nästa exempel

Förenkla #5^2 \cdot 3^4 \cdot 5^{-1}\cdot 3^{-2}#med hjälp av räknereglerna och svara i potensform.
#\,#

#\,#
Vi beräknar varje bas för sig:

#5^2 \cdot 3^4 \cdot 5^{-1}\cdot 3^{-2} = 5^{2-1}\cdot 3^{4-2}=5\cdot 3^2#

Nästa exempel

Förenkla med hjälp av räknereglerna

#(4\cdot 2)^3#
#\,#

#\,#
Här har vi en potens av en produkt och vi upphöjer då varje faktor var för sig.

#(4\cdot 2)^3 = 4^3 \cdot 2^3#

Ofta använder vi regeln "baklänges": #4^3\cdot2,5^3=(4\cdot2,5)^3=10^3#

Nästa exempel

Vilket värde har k om #2#^#2# = #4^k#?

\[\begin{array}{rcll}
\displaystyle
2^2 &=& (2^2)^k & \text{Vi skriver om } 4 \text{ som } 2^2\text{, så att vi får samma bas på båda sidor om likhetstecknet.}\\
2^2 &=& 2^{2k} & \text{Vi förenklar med hjälp av räknereglerna och jämför exponenterna.}\\
2 &=& 2k &\\
k &=& 1 &\\
\end{array}\]

Nästa exempel