Numeriska uttryck är beräkningar som bara innehåller siffertermer.

Elsa köper #3 # kastruller för #250 # kr styck, #2 # skålar för #84 # kr styck och en papperskasse för #5 # kr. Den totala kostnaden i kronor kan skrivas med ett numeriskt uttryck:

#250 \cdot 3 + 84 \cdot 2 + 5 #

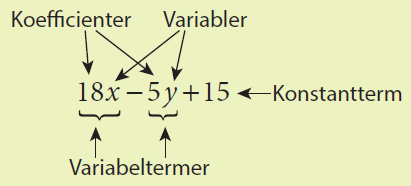
Algebraiska uttryck är uttryck som innehåller minst en bokstav.

Om Elsa i stället köper # x # stycken kastruller, # y # stycken skålar och en papperskasse för #5 # kr kan totalkostnaden skrivas:

I det algebraiska uttrycket är # x # och # y # variabler. Här betyder det att # x # och # y # kan anta olika värden. #250 x # och #84 y # är variabeltermer där siffrorna kallas koefficienter. #5 # är en konstantterm.

Uttryckets värde

Om # x = 8 # och # y = 5 # kan vi beräkna värdet av uttrycket ovan genom att ersätta # x # och # y # med de givna siffrorna:

#250 \cdot 8 + 84 \cdot 5 + 5 = 2 425 #

Kostnaden för #8 # kastruller, #5 # skålar och en plastkasse är #2 425 # kr.