Förenkling av uttryck Del II

1c 1. Aritmetik och algebra: 1.3 Uttryck

Förenkling av uttryck Del II

Vi multiplicerar en faktor före en parentes med varje term i parentesen och summerar efteråt.

#9 \cdot (5 + 2) = 9 \cdot 5 + 9 \cdot 2 = 45 + 18 = 63 #

Vi skriver ett generellt uttryck genom att använda a, b och # c # i stället för siffror:

# a ( b + c ) = ( b + c ) a = ab + ac #
#\,#

Kontroll

Utför multiplikationen utan att förenkla parentesen.

a) #\ 5 \cdot (3 + 4) #

b) #\ 6 \cdot (14 - 8)#

Svar

a) #\ 5 · 3 + 5 · 4 = 35#

b) #\ 6 · 14 - 6 · 8 = 84 - 48 = 36#

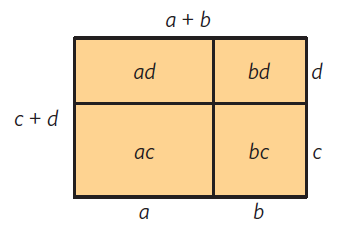
När vi ska förenkla ett uttryck med två parenteser efter varandra multipliceras varje term i den ena parentesen med varje term i den andra parentesen.

#( a + b )( c + d ) = ac + ad + bc + bd #

Vi kan förstå regeln med hjälp av en areaberäkning. Arean av hela rektangeln är lika stor som summan av de fyra delarna.

Vi kan också visa att regeln gäller med hjälp av ett numeriskt exempel:

#(12 - 3)(5 + 2) = 12 \cdot 5 + 12 \cdot 2 - 3 \cdot 5 - 3 \cdot 2 = 60 + 24 - 15 - 6 = 63 #

Om vi utför samma beräkning men först förenklar parenteserna får vi:

#(12 - 3)(5 + 2) = 9 \cdot 7 = 63 #

Resultaten är lika.

Regler vid parentesmultiplikation

# a ( b + c ) = ( b + c ) a = ab + ac #	En faktor multipliceras med varje term i en parentes.
#( a + b )( c + # d) #= ac + ad + bc + bd #	Varje term i en parentes multipliceras med varje term i den andra parentesen.

Multiplicera in faktorn i parentesen.

#3(5 - 4 x ) #

#3(5 - 4 x ) = 15 - 12 x #

Nästa exempel

Förenkla uttrycket

#6(2 x - 3) - 5(4 - 5 x ) #

#6(2 x - 3) - 5(4 - 5 x ) =#

#= 12 x - 18 - 20 + 25 x =#

#= 37 x - 38 #

Nästa exempel